Question

Four solid spheres each of diameter $\sqrt 5 cm$ and mass 0.5kg are placed with their centres at the corners of a square of side 4cm. The moment of inertia of the system about the diagonal of the square is $N \times {10^{ - 4}}Kg{m^2}$then N is?

Answer 1

Hint: The moment of inertia of a system of solid bodies about any axis is the sum of moments of inertia of individual bodies about that axis. The moment of inertia of a sphere of radius R about the centre of mass is \[I' = \dfrac{2}{5}M{R^2}\]

Complete Step by Step answer:
We know the moment of inertia of a body is given as $I = \sum\limits_i {{m_i}{r_i}^2} $
Now here we have 4 individual groups of masses. We know the moment of inertia of each of them individually but we are asked the combined moment of inertia.
we can split the summation in eqn(1) as \[I = {\left. {\sum\limits_i {{m_i}{r_i}^2} } \right|_A} + {\left. {\sum\limits_i {{m_i}{r_i}^2} } \right|_B} + {\text{ }}{\left. {\sum\limits_i {{m_i}{r_i}^2} } \right|_C} + {\left. {\sum\limits_i {{m_i}{r_i}^2} } \right|_D}\]
So we see that the total moment of inertia $I$ is the sum of individual moments of inertia : ${I_A}$, ${I_B}$, ${I_C}$, and ${I_D}$,
$I = {I_A} + {I_B} + {I_C} + {I_D}$

Here, we have 4 spheres placed at the corners of a square as shown in the diagram. Since the square is rotating about the diagonal, two of the spheres will be rotating along an axis passing through their centre of mass, but two of them are away from the axis and would rotate in circles.
Their distances from the axis is :
$\sqrt {{2^2} + {2^2}} = \sqrt 8 = 2\sqrt 2 cm$

Now, we know the moment of inertia of a sphere about an axis through the centre is :
\[I' = \dfrac{2}{5}M{R^2}\]

But for a sphere rotating at a distance $L$ away from the axis, the moment of inertia has to be found using the parallel axis theorem. According to this theorem, the moment of inertia of a body along any axis is the sum of its moment of inertia about a parallel axis passing through its centre of mass and the product of mass and square of distance from the axis.
${I_L} = {I_{com}} + M{L^2}$

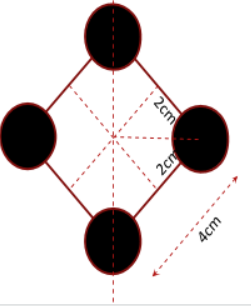
Now, we can find the moment of inertia of spheres A and B in the diagram as:
${I_A} = {I_B} = \dfrac{2}{5}M{R^2}$
Let's substitute the values given in the question into our equation
${I_A} = {I_B} = \dfrac{2}{5}0.5{\text{ }}{\left( {\dfrac{{\sqrt 5 }}{2}} \right)^2} = 0.25kgc{m^2}$

Similarly, for the masses C and D,
${I_C} = {I_D} = \dfrac{2}{5}M{R^2} + M{L^2}$

since we now know $L = 2\sqrt 2 cm$, we can substitute it in
\[{I_C} = {I_D} = \dfrac{2}{5}0.5{\text{ }}{\left( {\dfrac{{\sqrt 5 }}{2}} \right)^2} + 0.5{\left( {2\sqrt 2 } \right)^2} = 4.25\]
Now net moment of inertia is $I = {I_A} + {I_B} + {I_C} + {I_D}$
$I = 0.25 + 0.25 + 4.25 + 4.25 = 9kgc{m^2}$
Converting it to $kg{m^2}$gives :
\[9kg{\left( {{{10}^{ - 2}}m} \right)^2} = 9 \times {10^{ - 4}}Kg{m^2}\]
Comparing this with \[N \times {10^{ - 4}}Kg{m^2}\] gives \[N = 9\]. This is the required answer.

Note: Parallel axis theorem can only be applied if the moment of inertia about the centre of mass is known. If the moment of inertia about some other axis is given, we will first have to find the moment of inertia about the centre of mass and then use it to find the unknown moment of inertia.