Question

Four solid spheres, each of mass m and radius r are placed on the vertices of a square of side length a. The M.I of the system about an axis passing through the diagonal of the square will be?

Answer 1

Hint: We are given that the four spheres are placed on the vertices of the square. This means that two spheres lie on those vertices through which the axis of rotation passes through. Thus, we first have two spheres whose moment of inertia is equivalent to that of a solid sphere whose axis of rotation passes through their centre. As for the other two spheres that lie on the non-rotational diagonal, the moment of inertia will arise from their masses as well as their normal distance from the centre of the axis of rotation. Subsequently, the moment of inertia of the system will be the additive sum of moments about each sphere.

Formula used: MI of a solid sphere with axis of rotation through its centre: $I = \dfrac{2}{5}mr^2$

Complete step by step answer:
Given that we have four solid spheres, each of mass m and radius r, arranged on the vertices of a square with sides of length a, as shown in the figure. Let the axis of rotation AB be along the diagonal of the square.
Let us find the length of the diagonal. Using Pythagoras theorem on triangle 324, we get the length of the diagonal 32 to be $ = \sqrt{a^2+a^2} = \sqrt{2a^2} = a\sqrt{2}$.
The centre of the diagonal, which is the distance of each sphere from the centre of the square will be $r = \dfrac{a\sqrt{2}}{2}= \dfrac{a}{\sqrt{2}} $
Now, the moment of inertia (MI) of the system of spheres about the diagonal of square will be:
$I = I_2+I_3+I_1+I_4$, where each I corresponds to the MI of each sphere about this axis.
Let us find the MI of each sphere about the axis of rotation AB that is along one of the diagonals of the square.

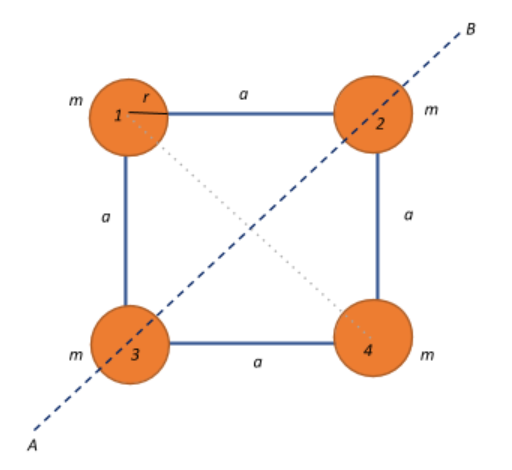
The MI of 2 and 3 will be the same and will be equivalent to the MI of a uniform solid sphere with the axis of rotation passing through its centre.
$I_2 = I_3 = \dfrac{2}{5}mr^2$
Now, the distance between each sphere 1 and 4 from the axis of rotation is $r=\dfrac{a}{\sqrt{2}}$. Therefore, the MI of spheres 1 and 4 will be the same since they’re at the same distances from AB, and is equivalent to the sum of MI of a solid sphere and the MI due to the distance of the sphere from the axis of rotation:
$I _1 = I_4 = \dfrac{2}{5}mr^2+m\left(\dfrac{a}{\sqrt{2}}\right)^2 = \dfrac{2}{5}mr^2+\dfrac{1}{2}ma^2$
Therefore, the net MI of the system of spheres about with axis of rotation AB is:
$I = 2 \times \left(\dfrac{2}{5}mr^2\right) + 2 \times \left(\dfrac{2}{5}mr^2+\dfrac{1}{2}ma^2\right)$
$\Rightarrow I = \dfrac{4}{5}mr^2 + \dfrac{4}{5}mr^2 + ma^2$
$\Rightarrow I = \dfrac{8}{5}mr^2 + ma^2$

Therefore, the M.I of the system about an axis passing through the diagonal of the square will be
$ I = \dfrac{8}{5}mr^2 + ma^2$

Note: Recall that the moment of inertia is dependent on the distribution of mass of the system about the axis of rotation, the position and orientation of the axis of rotation and the shape of the bodies constituting the system. This is why the moment of inertia of the spheres that lay along the axis of rotation turned out to be different from that of the spheres on the other vertices of the square.
The moment of inertia of this system would also be different if the axis of rotation was, say, about one of the sides of the square instead of through the diagonal. In such a case, the MI of the spheres lying along the axis of rotation would be $I = \dfrac{2}{5}mr^2$ each, and the MI of the spheres lying on the edges that are parallel to the axis of rotation would be $I = \dfrac{2}{5}mr^2 + ma^2$ each, and the net MI of the system would consequently be $I_{effective} = 2 \times \dfrac{2}{5}mr^2 + 2 \times \left(\dfrac{2}{5}mr^2 + ma^2\right) = \dfrac{8}{5}mr^2+2ma^2$.