Question

From 50 students taking examinations in Mathematics, Physics, and Chemistry. 37 passed in Mathematics, 24 in Physics, and 43 in Chemistry. At most 19 passed in Mathematics and Physics, at most 29 passed in Mathematics and Chemistry, and at most 20 passed in Physics and Chemistry. Find out the largest possible number that could have passed all three examinations.
A. 11
B. 12
C. 13
D. 14

Answer 1

Hint: We will first write all the given information in the question in the form of the sets and then we will apply the given condition that is the number of at most students passed in the two subjects. Then we will apply the inclusion formula that is: \[n\left( A\cup B\cup C \right)=n\left( A \right)+n\left( B \right)+n\left( C \right)-n\left( A\cap B \right)-n\left( A\cap C \right)-n\left( B\cap C \right)+n\left( A\cap B\cap C \right)\], after that we will compare the condition to the equation obtained by the above given formula and get the answer.

Complete step-by-step solution
Now, let M, P, and C is the sets of students taking examinations in Mathematics, Physics, and Chemistry, respectively.
So, it is given that:
37 passed in Mathematics, therefore: $n\left( M \right)=37$ and 24 passed in Physics, therefore: $n\left( P \right)=24$, and 43 passed in Chemistry, therefore: $n\left( C \right)=43$
Now, it is given that the total students taking the examination are 50, therefore: $n\left( M\cup P\cup C \right)=50$ .
Now it is given that at most 19 passed in Mathematics and Physics, therefore: $n\left( M\cap P \right)\le 19$, it is also given that at most 29 passed in Mathematics and Chemistry, therefore: $n\left( M\cap C \right)\le 29$, and finally it is given that at most 20 passed in Physics and Chemistry, therefore: $n\left( P\cap C \right)\le 20$.

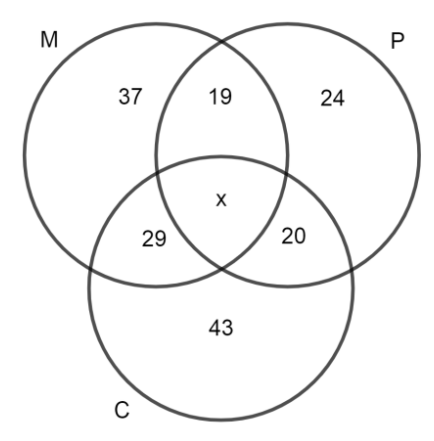
Now, we know that according to inclusion formula:
\[n\left( M\cup P\cup C \right)=n\left( M \right)+n\left( P \right)+n\left( C \right)-n\left( M\cap P \right)-n\left( M\cap C \right)-n\left( P\cap C \right)+n\left( M\cap P\cap C \right)\]Now, we will all put the values in this equation:
$\begin{align}
  & \Rightarrow 50=37+24+43-\left\{ n\left( M\cap P \right)+n\left( M\cap C \right)+n\left( P\cap C \right) \right\}+n\left( M\cap P\cap C \right) \\
 & \Rightarrow \left\{ n\left( M\cap P \right)+n\left( M\cap C \right)+n\left( P\cap C \right) \right\}=n\left( M\cap P\cap C \right)+104-50 \\
 & \Rightarrow \left\{ n\left( M\cap P \right)+n\left( M\cap C \right)+n\left( P\cap C \right) \right\}=n\left( M\cap P\cap C \right)+54\text{ }..........\left( 1 \right) \\
\end{align}$
Now, it is given that: $n\left( M\cap P \right)\le 19$, $n\left( M\cap C \right)\le 29$ and $n\left( P\cap C \right)\le 20$.
We will now add these, therefore: $n\left( M\cap P \right)+n\left( M\cap C \right)+n\left( P\cap C \right)\le 19+29+20$
Therefore, we will use equation 1 to replace the left hand side:
$n\left( M\cap P\cap C \right)+54\le 68\Rightarrow n\left( M\cap P\cap C \right)\le 14$.
Therefore, the largest possible number that could have passed all the three examinations is 14. Hence, the correct option is D.

Note: Remember that Venn diagrams help you picturise what is going on and deriving the appropriate statements, so always draw that for a better understanding of the examiner. The inclusion formula for union is important as there are three sets given, we did not have to be concerned about when there were only two sets. Here, you have to make sure that you consider the less than or equal to condition instead of less than, else you might choose a different option.