
From a uniform disk of radius
Answer
515.1k+ views
Hint: Assume that the mass per unit area of the uniform disc is
Formula used:
where
and
Complete step-by-step solution -
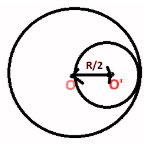
Given that,
Radius of uniform disc
Radius of the smaller disc
Let the mass per unit area of the original disc
Therefore mass of the uniform disc
And the mass of the small disc
Now as the small disc has been cut from the uniform disc, the remaining portion is considered to be a system of two masses.
The two masses are:
(negative sign indicating above that the portion is removed from the uniform disc)
Let
The relation between the centre of masses of two masses is give as:
Note: The relation between the centre of masses of two masses is calculated by the formula
Formula used:
where
and
Complete step-by-step solution -

Given that,
Radius of uniform disc
Radius of the smaller disc
Let the mass per unit area of the original disc
Therefore mass of the uniform disc
And the mass of the small disc
Now as the small disc has been cut from the uniform disc, the remaining portion is considered to be a system of two masses.
The two masses are:
(negative sign indicating above that the portion is removed from the uniform disc)
Let
The relation between the centre of masses of two masses is give as:
Note: The relation between the centre of masses of two masses is calculated by the formula
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

Why is steel more elastic than rubber class 11 physics CBSE

Explain why a There is no atmosphere on the moon b class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE




