
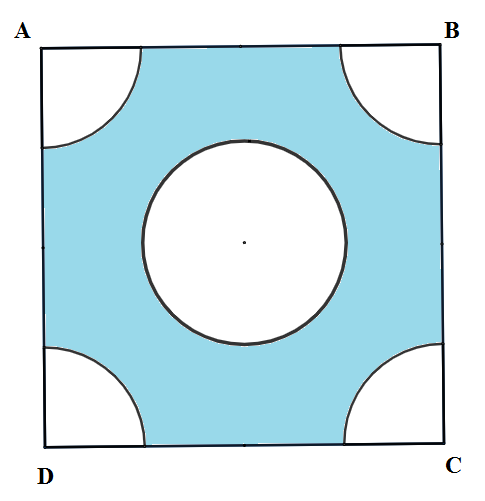
From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in fig. Find the area of the remaining portion of the square.

Answer
478.2k+ views
1 likes
Hint: We find the formula for the area of the square as
Complete step by step answer:
Let us observe the given figure.
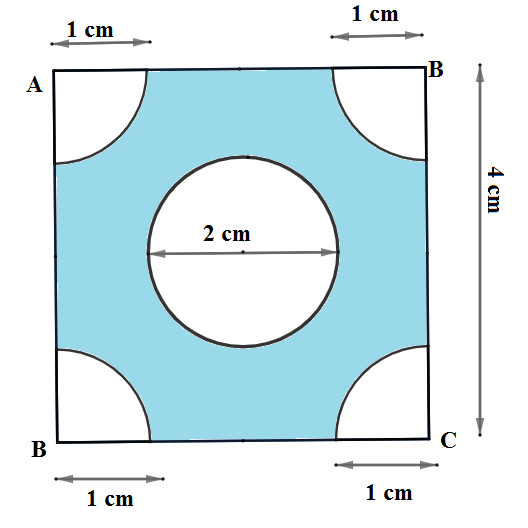
We are given the question that ABCD is square with length 4cm. So the area of the square is
We are also given in the question that at each corner A,B,C and D a quadrant of a circle of radius 1 cm is cut. We also see that the area of four quadrants at the four corners is equal. We know that the area of the one quadrant is one –fourth of the area of the circle. Let us find the area of one quadrant as
We are further given the question that a circle of diameter 2 cm is cut as shown in fig. So the radius of the circle is
We are asked to find the area of the remaining portion. We see that the remaining portion is obtained when we remove the four quadrant regions and the circular regions. We have the required area as;
We take the value of
So the area of the remaining portion is
Note:
We note that areas of congruent shapes are always equal and the quadrants of the circle are congruent when equal radii have. That is why the areas of four quadrants are equal. We also note that the question presumes that the center of the removed circle and the centre of the square (point of intersection of diagonals) coincide. We should always take care of units when calculating areas.
Complete step by step answer:
Let us observe the given figure.

We are given the question that ABCD is square with length 4cm. So the area of the square is
We are also given in the question that at each corner A,B,C and D a quadrant of a circle of radius 1 cm is cut. We also see that the area of four quadrants at the four corners is equal. We know that the area of the one quadrant is one –fourth of the area of the circle. Let us find the area of one quadrant as
We are further given the question that a circle of diameter 2 cm is cut as shown in fig. So the radius of the circle is
We are asked to find the area of the remaining portion. We see that the remaining portion is obtained when we remove the four quadrant regions and the circular regions. We have the required area as;
We take the value of
So the area of the remaining portion is
Note:
We note that areas of congruent shapes are always equal and the quadrants of the circle are congruent when equal radii have. That is why the areas of four quadrants are equal. We also note that the question presumes that the center of the removed circle and the centre of the square (point of intersection of diagonals) coincide. We should always take care of units when calculating areas.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Where did Netaji set up the INA headquarters A Yangon class 10 social studies CBSE

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE




