
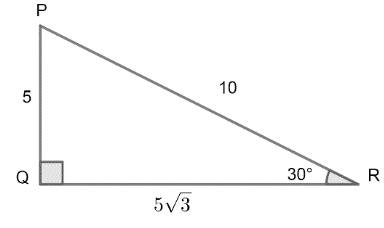
From the following figure find the value of

Answer
528k+ views
Hint: We will calculated the value of
Complete step-by-step answer:
It is given in the question that PQR is a right angle triangle which is right angled at Q. Now, we will try to find out the value of
This right angled triangle PQR is showing the given conditions in question.
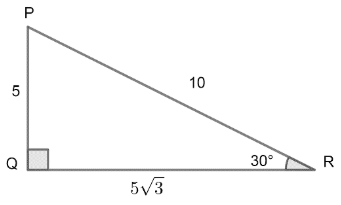
Now, we know that in this right angled triangle PQR, there are some specific names of each side as PQ is called height of the triangle, QR is called the base of the triangle, and PR is called the hypotenuse of the triangle PQR.
Also, It is given that PQ or perpendicular height of the triangle is of 5 units, QR or the base of the given triangle is of
We know that from Pythagoras Theorem can be applied to a right triangle. So, we have the theorem as,
Also, we have Base =
Thus, LHS = RHS
Now, we know that
Also, we have here
Similarly, now we will calculate
Also, we have here
Now, we will calculate the value of
Here, we know that
Thus, in triangle PQR, we get
Note: If the angle and one side is given then also we can calculate all the values
So, using this method we can calculate all the values required in a triangle. We can also calculate value of
Thus, from this method also we get
Complete step-by-step answer:
It is given in the question that PQR is a right angle triangle which is right angled at Q. Now, we will try to find out the value of
This right angled triangle PQR is showing the given conditions in question.

Now, we know that in this right angled triangle PQR, there are some specific names of each side as PQ is called height of the triangle, QR is called the base of the triangle, and PR is called the hypotenuse of the triangle PQR.
Also, It is given that PQ or perpendicular height of the triangle is of 5 units, QR or the base of the given triangle is of
We know that from Pythagoras Theorem can be applied to a right triangle. So, we have the theorem as,
Also, we have Base =
Thus, LHS = RHS
Now, we know that
Also, we have here
Similarly, now we will calculate
Also, we have here
Now, we will calculate the value of
Here, we know that
Thus, in triangle PQR, we get
Note: If the angle and one side is given then also we can calculate all the values
So, using this method we can calculate all the values required in a triangle. We can also calculate value of
Thus, from this method also we get
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Where did Netaji set up the INA headquarters A Yangon class 10 social studies CBSE

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What are the public facilities provided by the government? Also explain each facility




