Question

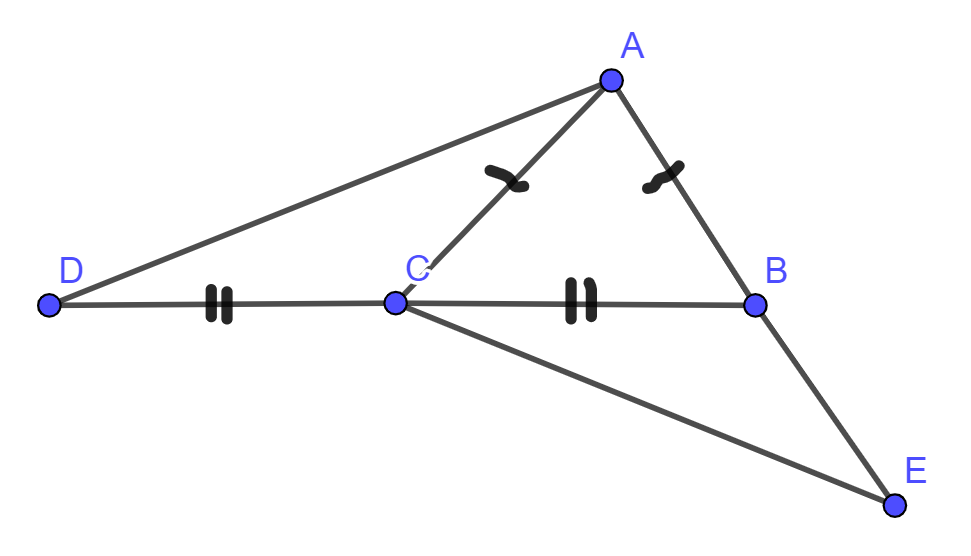
From the following we can say: AD = CE. State TRUE or FALSE.

Answer 1

Hint: Here in the given question we need to know whether the given side AD = CE. To solve this problem we need to know the concept of the congruence of triangles. We know that congruent means two triangles must have the same shape and size when superimposed over one other. In congruent triangles the corresponding sides and angles should be equal.

Complete step by step answer:
In the given question to find whether the given sides are equal or not to know that we will first consider the triangle ABC in which the sides AC and AB are equal and thus using the rule of isosceles triangle we show that
In \[\vartriangle \] ABC
\[ \Rightarrow \] AB = AC (given)
\[ \Rightarrow \]\[\angle ACE = \angle ABC\] --------- (1)
From the properties of isosceles triangle, we know that the two angles opposite to the equal sides are congruent to each other. Thus \[\angle ACB = \angle ABC\]= x
Now to know the \[\angle CBE\] using linear pair property we get
\[ \Rightarrow \]\[\angle ABC + \angle CBE = {180^ \circ }\] ----------- (2)
On substituting the unknown value to be x in equation (2)
\[ \Rightarrow \]\[x + \angle CBE = {180^ \circ }\]
On rearranging the equation we get
\[ \Rightarrow \] \[\angle CBE = {180^ \circ } - x\] --------- (3)
Considering\[\vartriangle ACD\], using linear pair property
\[ \Rightarrow \]\[\angle ACB + \angle ACD = {180^ \circ }\] ---------- (4)
On rearranging equation (4)
\[ \Rightarrow \]\[\angle ACD = {180^ \circ } - x\] --------- (5)
From equation (3) and (5)
\[ \Rightarrow \]\[\angle ACD = \angle CBE\] --------- (6)
Now considering the triangles \[\vartriangle ACD\]and \[\vartriangle ECB\]
\[ \Rightarrow \]AC = BC (given)
\[ \Rightarrow \]DC = CB (given)
\[ \Rightarrow \]\[\angle ACD = \angle CBE\] from equation (6)
From SAS congruence rule
\[ \Rightarrow \] \[\vartriangle ACD\,\, \cong \,\,\vartriangle ECB\]
Hence using corresponding parts of congruent triangles we have
\[ \Rightarrow \]AD = CE
Thus the given statement is true.

Note:
Remember there are 4 different criteria of congruence. When all the three corresponding sides of two triangles are equal then the triangles are said to be congruent under (SSS) side-side-side congruence criteria. Similarly triangles having two sides including angle between them is said to be congruent under SAS congruence criteria.