
From the point on a bridge across a river, the angles of depressions of the banks on opposite sides of the river are \[{{30}^{\circ }}\] and \[{{45}^{\circ }}\], respectively. If the bridge is at a height of 3 m from the banks, find the width of the river.
Answer
492k+ views
Hint: Consider the maximum height as AB and draw the angle of depression at two different points and apply \[\tan \theta \] to the two right angled triangles and we will get two equations and then we have to compute the maximum height from which he falls.
Complete step-by-step answer:
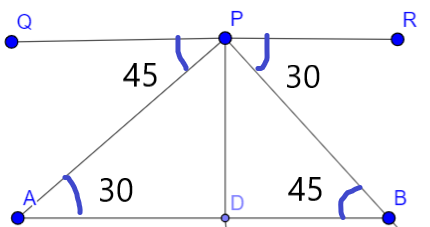
Let width of river =AB
And bridge is at height of 3m from banks So, DP=3m
Angel of depression of banks on the opposite sides of the river are \[{{30}^{\circ }}\] and \[{{45}^{\circ }}\].
\[\begin{align}
& \angle QPA={{30}^{\circ }} \\
& \angle RPB={{45}^{\circ }} \\
\end{align}\]
Now in triangle PAD
\[\tan {{30}^{\circ }}={PD}{AD}\]
\[{1}{\sqrt{3}}={3}{AD}\]
\[AD=3\sqrt{3}\]. . . . . . . . . . . . . . . . . . . . . . . (1)
Now in triangle PBD
\[\tan {{45}^{\circ }}={PD}{DB}\]
\[1={3}{DB}\]
\[DB=3\]. . . . . . . . . . . . . . . . . . . . . . . . . . (2)
Width of river = \[AB=AD+DB\]
Hence width of river \[=3\left( \sqrt{3}+1 \right)\]
Note: If the object observed by the observer is below the level of the observer, then the angle formed between the horizontal line and the observer’s line of sight is called the angle of depression. As the person moves from one point to another angle of depression varies.
Complete step-by-step answer:

Let width of river =AB
And bridge is at height of 3m from banks So, DP=3m
Angel of depression of banks on the opposite sides of the river are \[{{30}^{\circ }}\] and \[{{45}^{\circ }}\].
\[\begin{align}
& \angle QPA={{30}^{\circ }} \\
& \angle RPB={{45}^{\circ }} \\
\end{align}\]
Now in triangle PAD
\[\tan {{30}^{\circ }}={PD}{AD}\]
\[{1}{\sqrt{3}}={3}{AD}\]
\[AD=3\sqrt{3}\]. . . . . . . . . . . . . . . . . . . . . . . (1)
Now in triangle PBD
\[\tan {{45}^{\circ }}={PD}{DB}\]
\[1={3}{DB}\]
\[DB=3\]. . . . . . . . . . . . . . . . . . . . . . . . . . (2)
Width of river = \[AB=AD+DB\]
Hence width of river \[=3\left( \sqrt{3}+1 \right)\]
Note: If the object observed by the observer is below the level of the observer, then the angle formed between the horizontal line and the observer’s line of sight is called the angle of depression. As the person moves from one point to another angle of depression varies.
Recently Updated Pages
Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Why is there a time difference of about 5 hours between class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

Explain the Treaty of Vienna of 1815 class 10 social science CBSE

A Paragraph on Pollution in about 100-150 Words




