Question

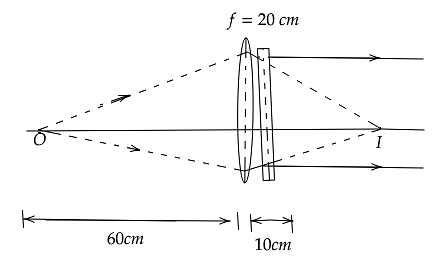
From the ray diagram show, calculate the focal length of the concave lens.

Answer 1

Hint: We should understand the lens formula according to the above diagram, so we know the focal length and object distance value. a ray diagram, one helpful tool that is sometimes used to portray this concept is known. So, we use the concave lens formula to find the picture distance, and we also understand the definition of focal length to evaluate the given problem.
Useful formula:
The lens formula
$\dfrac{1}{f} = \dfrac{1}{u} + \dfrac{1}{v}$
$f = $ focal length
$u = $ object distance
$v = $image distance

Complete answer:
Given by,
$u = 60\,cm$
$f = 20\,cm$
Above diagram is represented as,
A concave lens is a lens that has at least one inward-curving surface. It is a diverging lens, which means that light rays that have been refracted into it are spread out. At its middle, a concave lens is thinner than at its edges and is used to correct short-sightedness (myopia).
According to the lens formula,
$\dfrac{1}{f} = \dfrac{1}{u} + \dfrac{1}{v}$
substituting the given value in above equation,
We get,
$\dfrac{1}{v} + \dfrac{1}{{60}} = \dfrac{1}{{20}}$
On simplifying the above equation,
Here,
$\dfrac{1}{v} = \dfrac{1}{{30}}$
Now,
the relationship between the distance of an image
$v = 30\,cm$
Hence,
Focal length of concave lens is $30 - 10 = 20cm$

Note:
Since the distance between the concave mirror pole 0 and the focus F is the concave mirror's focal length. Therefore, it is possible to approximate the focal length of a concave mirror by obtaining a real image of a distant object at its focal point. A ray diagram that traces the path taken by light for a person to view a point in an object's image.