Question

From the top of a cliff 200ft. high, the angle of depression of the top and bottom of the tower are observed to be 30 and 60 respectively. The height of the tower is

Answer 1

Hint: Angle of depression is given, on the basis of this we have to draw diagrams, then conditions will be forms, after solving conditions and equations, we will get the answer.

Complete step-by-step answer:

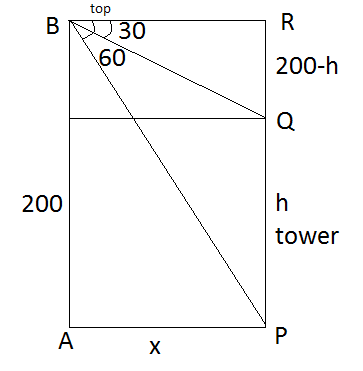
Let PQ $$ = h$$ be the height of tower angles of depression of Q and P are $${30^o}$$ and $${60^o}$$ as seen from top B of cliff AB of height $$200$$ ft.
Let AP$$ = x$$ .
$$\eqalign{
  & 200 - h = x\tan 30 = \dfrac{x}{{\sqrt 3 }};\vartriangle BQR \cr
  & 200 = x\tan 60 = \sqrt 3 x;\vartriangle BPR \cr} $$
Dividing, we get
$\Rightarrow$ $$\dfrac{{200 - h}}{{200}} = \dfrac{1}{3}$$
$\Rightarrow$ $$3\left( {200 - h} \right) = 200$$
 $$\eqalign{
  &\Rightarrow 400\; = 3h\; \cr
  & \Rightarrow h = \dfrac{{400}}{3}\;ft. \cr} $$
Note: The angle of elevation of an object as seen by an observer is the angle between the horizontal and the line from the object to the observer’s eye. Don’t get confused between the angle of elevation and depression.