Question

What is the general equation of a parabola whose vertex is \[\left( {0,\,2} \right)\] and vertex is above focus?

Answer 1

Hint: Here first we will observe that the x coordinate of vertex is zero. So, the axis of the parabola should be $y$ axis. Next it is given that the vertex is above focus, so it is an upward parabola which is cutting the y axis at \[\left( {0,\,2} \right)\]. Therefore, if we represent the equation of parabola as $y = a{\left( {x - h} \right)^2} + k$, then h should be zero here and a should be negative.

Complete step by step answer:
In the above question, it is given that there is a parabola whose vertex is \[\left( {0,\,2} \right)\] and the vertex is above focus. Therefore, we can represent the above parabola as,

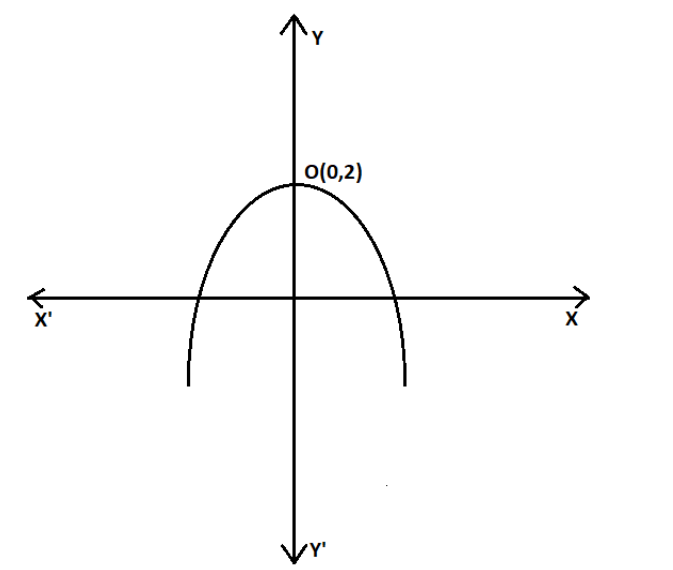
We can write a parabola in its standard form as $y = a{\left( {x - h} \right)^2} + k$, where $x - h = 0$ is the axis of symmetry and $\left( {h,k} \right)$ is the vertex. So, basically there are four things to note here:
- Axis of symmetry is perpendicular to the directrix and passes through the focus and hence the axis of symmetry is $x = 0$.
- Hence, the axis of symmetry and the directrix cut each other at $\left( {0,4} \right)$.
- Vertex is always midway between the directrix and the focus and hence the vertex is $\left( {0,2} \right)$.
- As vertex (and directrix) is above focus, parabola will have a maxima at vertex and a is negative.

Hence, we can write the standard form of equation of parabola as $y = a{\left( {x - 0} \right)^2} + 2$ or $y = a{\left( x \right)^2} + 2$ , where $a < 0$.

Note:Here we should be careful while deciding that it is an upward parabola or a downward parabola. If the vertex is above the focus, then it is an upward parabola and if the vertex is below the focus, then it is a downward parabola. Also, if some constant term is subtracted or added in the equation, then its vertex should not be the origin. There should be some other point.