Question

How to get the surface area of a cone using integral calculus \[?\]

Answer 1

Hint:This question describes the operation of finding the area of a circle and lateral surface of the cone. We need to know the basic integration and differentiation. Also, we need to know the process of finding\[\sin \theta \], \[\cos \theta \]and \[\tan \theta \]from the triangle.

We need to know trigonometric conditions to make an easy calculation.

Complete step by step solution:

In the given question we have to find the total surface area of a cone using integral calculus. For finding the surface area the following figure will help us,

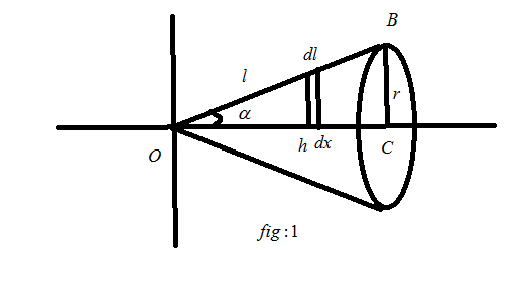
In the above figure,

\[C\] is the center of the bottom of the cone,

\[l\]is the length of slant edge in the cone,

\[h\]is the vertical height of the cone,

\[\alpha \] is the angle between \[OC\]and \[OB\],

\[dl\] is the small part of the slant edge,

\[dx\] is the small part of vertical height,

\[r\]is the radius of the bottom cone.

We know that the bottom of the cone is a circle. So, we have to find the area of the circle. For finding the area of the circle we assume the following figure,

The above figure was drawn with the reference of\[fig:1\]. From the\[fig:2\], we get the following equation

\[{x^2} + {y^2} = {r^2} \to \left( 1 \right)\] (By Pythagoras theorem)

The above equation can also be written as

\[{y^2} = {r^2} - {x^2}\]

\[y = \sqrt {{r^2} - {x^2}} \]

The area of the circle,

\[{A_{circle}}\]=\[\int {\sqrt {{r^2} - {x^2}} } dx\]

Let’s take\[{r^2}\]it as a common term, so we get

\[{A_{circle}} = \int {\sqrt {{r^2}\left( {1 - \dfrac{{{x^2}}}{{{r^2}}}} \right)} dx} \]

We know that\[\sqrt {{r^2}} = r\]

\[{A_{circle}} = r\int {\sqrt {\left( {1 - \dfrac{{{x^2}}}{{{r^2}}}} \right)} dx} \to \left( 2 \right)\]

If we consider the limit between\[ - r\]and\[r\] we can evaluate the area of half of the circle.
From\[fig:2\]we get the following values,

\[
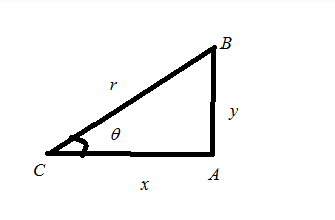
\cos \theta = \dfrac{{adj}}{{opposite}} = \dfrac{x}{r} \\

\dfrac{x}{r} = {\cos ^2}\theta = 1 - {\sin ^2}\theta \\
\]

\[\theta = arc\operatorname{Cos} \left( {\dfrac{x}{r}} \right)\]

Let’s take\[x = - r\]

\[\theta = arc\operatorname{Cos} \left( {\dfrac{{ - r}}{r}} \right)\]
\[\theta = arc\operatorname{Cos} \left( { - 1} \right)\]

We know that, \[arc\operatorname{Cos} ( - 1) = \pi \]

So, \[\theta = \pi \]

Let’s take \[x = r\]

\[\theta = arc\operatorname{Cos} \left( {\dfrac{r}{r}} \right)\]
\[\theta = arc\operatorname{Cos} \left( 1 \right)\]

We know that, \[arc\operatorname{Cos} (1) = 0\]

So, \[\theta = 0\]

We know that,

\[\cos \theta = \dfrac{x}{r}\]

Let’s differentiate the above equation, we get

\[ - \sin \theta d\theta = \dfrac{1}{r}dx\]
So, we get
\[

\dfrac{{dx}}{r} = - \sin \theta d\theta \\
dx = - r\sin \theta d\theta \\
\]

So, the equation\[\left( 2 \right)\]is,

\[{A_{circle}} = r\int {\sqrt {\left( {1 - \dfrac{{{x^2}}}{{{r^2}}}} \right)} dx} \]

(For finding the area of half of the circle the limit will be\[\pi to0\].)

Let’s substitute \[\dfrac{{{x^2}}}{{{r^2}}} = 1 - {\sin ^2}\theta ,dx = - r\sin \theta d\theta \]in the above equation, we get

\[
\dfrac{1}{2}{A_{circle}} = r\int\limits_\pi ^0 {\sqrt {1 - (1 - {{\sin }^2}\theta )} ( - r\sin \theta
d\theta )} \\

\dfrac{1}{2}{A_{circle}} = r\int\limits_\pi ^0 {\sqrt {1 - 1 + {{\sin }^2}\theta } ( - r\sin \theta
d\theta )} \\

\]

Here, \[r\]is constant, so it can be taken to the outside of the interval.

\[\dfrac{1}{2}{A_{circle}} = - {r^2}\int\limits_\pi ^0 {\sqrt {{{\sin }^2}\theta } (\sin \theta d\theta }
)\]

\[\dfrac{1}{2}{A_{circle}} = - {r^2}\int\limits_\pi ^0 {\sin \theta .\sin \theta d\theta } \]

\[\dfrac{1}{2}{A_{circle}} = - {r^2}\int\limits_\pi ^0 {{{\sin }^2}\theta d\theta } \]

We know that, \[{\sin ^2}\theta = \dfrac{{1 - \cos 2\theta }}{2}\]. So, we get

\[\dfrac{1}{2}{A_{circle}} = - {r^2}\int\limits_\pi ^0 {\dfrac{{1 - \cos 2\theta }}{2}d\theta } = -

{r^2}\int\limits_\pi ^0 {\left( {\dfrac{1}{2} - \dfrac{{\cos 2\theta }}{2}} \right)d\theta } \]

From equation\[\left( 1 \right)\]

\[{x^2} + {y^2} = {r^2} \to \left( 3 \right)\]

Let’s differentiate the above equation, we get

\[2xdx + 2ydy = 2rdr\]

In the above equation\[r\]is constant so, \[dr = 0\]. So, the above equation becomes,
\[2xdx + 2ydy = 0\]
\[

2xdx = - 2ydy \\
\dfrac{{dy}}{{dx}} = \dfrac{{ - 2x}}{{2y}} = \dfrac{{ - x}}{y} \to \left( 4 \right) \\
\]

From equation\[\left( 1 \right)\]

\[
{y^2} = {r^2} - {x^2} \\
y = \sqrt {{r^2} - {x^2}} \\
\]

By substituting the above-mentioned value in the equation\[\left( 4 \right)\]we get,

\[\dfrac{{dy}}{{dx}} = \dfrac{{ - x}}{{\sqrt {{r^2} - {x^2}} }}\]

The arc length L is
\[L = \int {ds} \]

Here, \[ds = \sqrt {1 + {{\left( {\dfrac{{dy}}{{dx}}} \right)}^2}} dx\]

Let’s substitute the\[\dfrac{{dy}}{{dx}}\]value in the above equation, we get

\[
ds = \sqrt {1 + {{\left( {\dfrac{{ - x}}{{\sqrt {{r^2} - {x^2}} }}} \right)}^2}} dx \\

ds = \sqrt {1 + \dfrac{{{x^2}}}{{{r^2} - {x^2}}}} dx \\
\]

\[
ds = \sqrt {\dfrac{{{r^2} - {x^2} + {x^2}}}{{{r^2} - {x^2}}}} dx \\

ds = \sqrt {\dfrac{{{r^2}}}{{{r^2} - {x^2}}}} dx \\
\]

Half of the circumference of the circle is given below,

\[L = \int\limits_{ - r}^r {ds} \]

By substituting the value of\[ds\] we get,

\[L = \int\limits_{ - r}^r {\sqrt {\dfrac{{{r^2}}}{{{r^2} - {x^2}}}} } dx\]

We know that, \[x = r\cos \theta \], \[dx = - r\sin \theta d\theta \]so, the above equation becomes

\[L = \int\limits_\pi ^0 {\sqrt {\dfrac{{{r^2}}}{{{r^2} - {x^2}}}} } \left( { - r\sin \theta } \right)d\theta
\]

\[L = \int\limits_\pi ^0 {\sqrt {\dfrac{{{r^2}}}{{{r^2} - {{\left( {r\cos \theta } \right)}^2}}}} } \left( { - r\sin \theta } \right)d\theta \]

\[L = \int\limits_\pi ^0 {\sqrt {\dfrac{{{r^2}}}{{{r^2}\left( {1 - {{\cos }^2}\theta } \right)}}} } \left( { - r\sin \theta } \right)d\theta \]

We know that, \[1 - {\cos ^2}\theta = {\sin ^2}\theta \]so, the above equation become,

\[L = \int\limits_\pi ^0 {\sqrt {\dfrac{{{r^2}}}{{{r^2}\left( {{{\sin }^2}\theta } \right)}}} } \left( { - r\sin \theta } \right)d\theta \]

\[L = - r\int\limits_\pi ^0 {\dfrac{1}{{\sin \theta }}} .\sin \theta d\theta \]
\[L = - r\int\limits_\pi ^0 1 d\theta \]

\[
L = - r\left[ \theta \right]_\pi ^0 = - r\left[ {0 - \pi } \right] \\
L = \pi r \\
\]

So, the full circumference of the circle is\[2L = 2\pi r\]

So, the lateral surface area of the cone
\[S = \int\limits_0^h {2\pi f\left( x \right)} dl\]
Here,\[y = f\left( x \right)\]

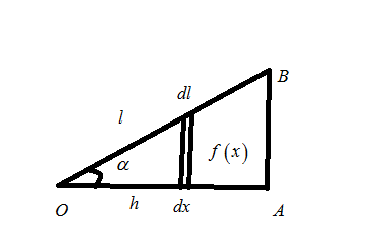
From the given figure

\[
\cos \alpha = \dfrac{h}{l} \\
l = \dfrac{h}{{\cos \alpha }} \\
dl = \dfrac{{dh}}{{\cos \alpha }} = \dfrac{{dx}}{{\cos \alpha }} \\
\tan \alpha = \dfrac{r}{h} = \dfrac{{f\left( x \right)}}{x} \\
\]
\[f\left( x \right) = x\tan \alpha \]

By using the above values we get,

\[S = \int\limits_0^h {2\pi x\tan \alpha \dfrac{{dx}}{{\cos \alpha }}} \]

\[S = 2\pi \dfrac{{\tan \alpha }}{{\cos \alpha }}\int\limits_0^h {xdx} \]
\[

S = 2\pi \dfrac{{\left( {\dfrac{r}{h}} \right)}}{{\left( {\dfrac{h}{l}} \right)}}\left[ {\dfrac{{{x^2}}}{2}}
\right]_0^h \\

S = 2\pi \left( {\dfrac{{rl}}{{{h^2}}}} \right)\left[ {\dfrac{{{h^2}}}{2} - \dfrac{{{0^2}}}{2}} \right]
\\

S = 2\pi r \\
\\
\]

So, the total surface area of the cone\[ = \]total surface area of the circle\[ + \]total surface area of the lateral surface.

The total surface area of the cone=\[\pi {r^2} + 2\pi r\]

Note: We have to consider the bottom of the cone as a circle. At first, we want to find the area of a circle, and next, we want to find the area of the lateral surface. Also, note that the integral of \[\cos \theta \]is\[\sin \theta \] and the differentiation of \[\cos \theta \]is\[ - \sin \theta \]. If a constant term is present inside the integral, we can take the term outside of the integral.