Question

Give the location of the centre of mass of a (i) sphere, (ii) cylinder, (iii) ring, and (iv) cube, each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body ?

Answer 1

Hint: For each and every uniform figure, which has uniform mass density, the center of mass will lie on the point where the symmetrical axis intersects with another symmetrical axis.

Complete step-by-step answer:
For sphere,
We know that center of mass lies on the symmetrical axis,
A sphere is a uniform figure hence center of mass will lie where the symmetrical axis intersects with another symmetrical axis.

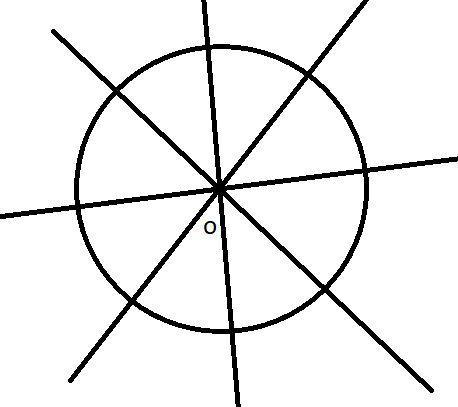
Here the lines drawn are the symmetrical lines, or random diameter for the sphere
O is the point where the center of mass lies.
For Cylinder,
We know that center of mass lies on the symmetrical axis,
A cylinder is a uniform figure hence center of mass will lie where the symmetrical axis intersects with another symmetrical axis.

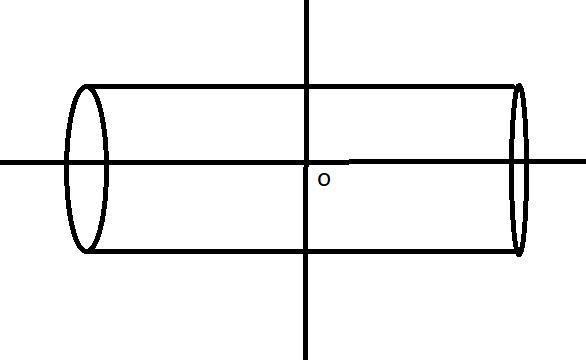
Here the lines drawn are the symmetrical lines, O is the point where the center of mass lies.
For the ring,
We know that center of mass lies on the symmetrical axis,
A ring is a uniform figure hence center of mass will lie where the symmetrical axis intersects with another symmetrical axis.
Symmetrical axes are lies drawn on an object through which when we cut the object we get two parts of the object exactly symmetrical.

Hence in the above figure we see that the center of mass lies outside the body of the ring.
O is the point where the center of mass lies.
For a cube, we can say from the above observations that the center of mass will lie on the geometrical center of the body.
The center of mass for the body is not necessary that it will be on the body just in case of the ring the center of mass is outside the body in the middle of the ring where it is hollow.

Note: Symmetrical axis are lines drawn on an object through which when we cut the object we get two parts of the object exactly symmetrical to each other. It is not necessary that the center of mass of the body will lie on the body; it can lie outside the body also.