Question

Give the prime factorization of the following number $136$ .

Answer 1

Hint: We will prime factorise by the factor tree method. we can see that the number $136$ is first factored into two numbers $4$ and $34$ . Again, $4$ and $34$ are factored into their factors. $4$ has the prime factor $2$ and $34$ has the prime factors $17$ and $2$ . Summing up all the prime factors, we get the prime factorisation.

Complete step by step answer:
In this problem, we need to find out the prime factorisation of the number $136$ . We will do so by the factor tree method. At first, we consider the given number as the base of the tree. We will then write down the pair of factors in the branches form of a tree. We will again factorise the composite factors and write down the factor pairs in the branches form of a tree. We will repeat this step until we have found the prime factors of all the composite factors.

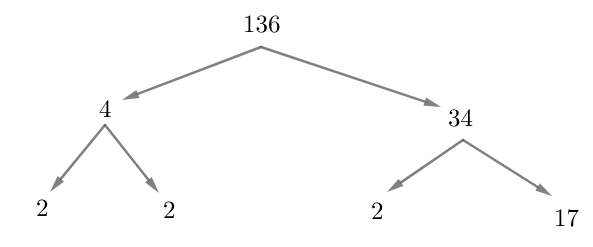
In the above figure, we can see that the number $136$ is first factorised into two numbers $4$ and $34$ . Again, $4$ and $34$ are factored into their factors. $4$ has the prime factor $2$ and $34$ has the prime factors $17$ and $2$ . Thus, $2,2,2,17$ form the last branch of the factor tree.
Thus, we can conclude that the prime factorisation of $136$ is $2\times 2\times 2\times 17$ .

Note: Prime factorisation of a number can also be done by the long division method. Here, we keep on dividing the number by its smallest prime divisor until the number that we are left with is a prime number itself. So,
$\begin{align}
  & 2\left| \!{\underline {\,
  136 \,}} \right. \\
 & 2\left| \!{\underline {\,
  68 \,}} \right. \\
 & 2\left| \!{\underline {\,
  34 \,}} \right. \\
 & ~~~~17 \\
\end{align}$
This gives the same result.