Question

Given a line and a point, not on the line, there is one and only …… line which passes through the given point and is …… to the given line.
A). One, parallel
B). One, perpendicular
C). Two, parallel,
D). Two, perpendicular

Answer 1

Hint: When given a line and a point, not on the line, there is one and only one line which passes through the given point. These lines are parallel or perpendicular to the given line. Based on the slopes and their properties we can say the above statement.

Complete step-by-step solution -

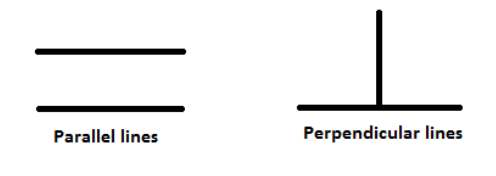
Parallel Lines: Parallel lines are lines in a plane which do not meet; that is, two straight lines in a plane that do not intersect at any point are said to be parallel
Examples: In real life, while railroad tracks, the edges of sidewalks and streets go up and down hills and around curves.
Properties of Parallel Lines
a). The corresponding angles are equal.
b). The vertically opposite angles are equal.
c). The alternate interior angles are equal.
d). The alternate exterior angles are equal.
e). The pair of interior angles on the same side of the transversal is supplementary.
If the slope of the two lines is the same, the two lines are parallel. If the slopes of two lines are ${{\text{m}}_1}{\text{ and }}{{\text{m}}_2}$, then for parallel lines the slopes are equal; that is, ${{\text{m}}_1}{\text{ = }}{{\text{m}}_2}$

Perpendicular Lines: The property of being perpendicular is the relationship between two lines which meet at right angles. Or we can say, a line is said to be perpendicular to another line if the two lines intersect at a right angle.
Examples: Perpendicular lines can be observed on floor tiles, on fences, on traffic signs or on furniture.
Properties of perpendicular lines
i). These lines always intersect at right angles.
ii). If two lines are perpendicular to the same line, they are parallel to each other and will never intersect.

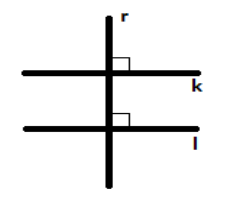
iii). Adjacent sides of a square and a rectangle are always perpendicular to each other.
iv). Sides of the right-angled triangle enclosing the right angle are perpendicular to each other.
If the product of the slopes is -1, then the lines are perpendicular. If the slopes of two lines are ${{\text{m}}_1}{\text{ and }}{{\text{m}}_2}$ and the product of their slopes, ${{\text{m}}_1} \times {{\text{m}}_2} = - 1$ then the lines are called as perpendicular lines.
$\therefore $With given a line and a point, not on the line, there is one and only one line which passes through the given point and is parallel or perpendicular to the given line.

Note: We can also prove using mathematically or through some construction by showing only one line passes through the point that is perpendicular to the line. And using Parallel postulate in Euclid’s geometry we can prove that only one line can be passed through the point and that it is parallel to it.