Question

Given the two ordered pairs (1, - 2) and (3, - 8), how do you write the equation of the line in slope intercept form.

Answer 1

Hint: To solve this question we will take the help of $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ and $m=\dfrac{y-{{y}_{1}}}{x-{{x}_{1}}}$. Also, we will get the equation of a line which is given by y = mx + c. Here, m is the point slope and c is the y intercept. Since, we have two ordered pairs of (1, - 2) and (3, - 8) so, we will use them for substitution in both formulas of m and after equating them we will compare the resultant equation to the equation of line.

Complete step-by-step answer:
The slope is represented by m and its value is obtained by the formula $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$. Since, the points given to us are (1, - 2) and (3, - 8) so, we will substitute these points in formula $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$. We will substitute these points by taking ${{x}_{1}}=1,{{y}_{1}}=-2,{{x}_{2}}=3,{{y}_{2}}=-8$. Therefore, we will consider the following figure and solve it accordingly,

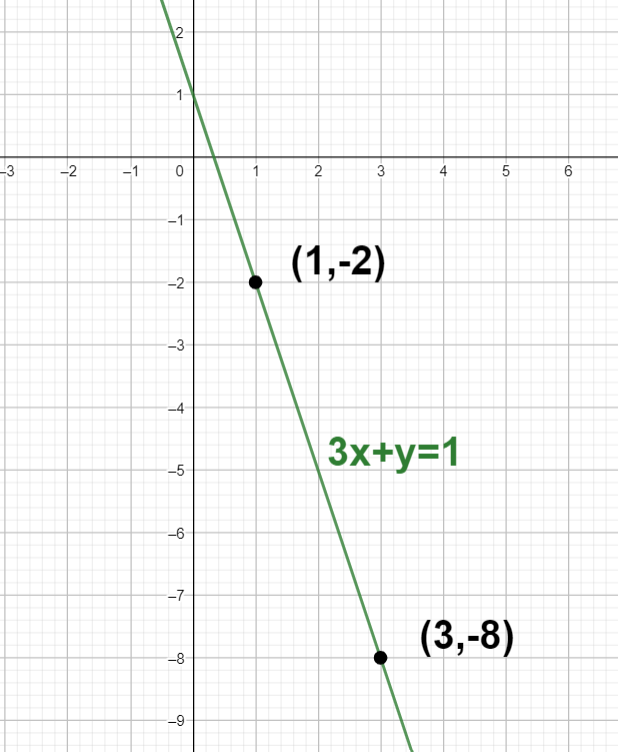
$\begin{align}
  & m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \\
 & \Rightarrow m=\dfrac{-8-\left( -2 \right)}{3-1} \\
 & \Rightarrow m=\dfrac{-8+2}{2} \\
 & \Rightarrow m=\dfrac{-6}{2} \\
 & \Rightarrow m=-3\,...(i) \\
\end{align}$
After this we will use the formula of slope also represented by m and its value will be calculated by $m=\dfrac{y-{{y}_{1}}}{x-{{x}_{1}}}$. Now, we will substitute the values of points in it to get \[m=\dfrac{y-\left( -2 \right)}{x-1}=\dfrac{y+2}{x-1}\,...(ii)\].
Since, equation (i) and equation (ii) are equal therefore, we get $\dfrac{y+2}{x-1}=-3$ and after applying cross multiplication we get,
$\begin{align}
  & \Rightarrow y+2=-3\left( x-1 \right) \\
 & \Rightarrow y+2=-3x+3 \\
\end{align}$
Now, we will keep the variables on the left side of the equation and the constant on the right side of the equation. Thus, we get
$\begin{align}
  & 3x+y=3-2 \\
 & \Rightarrow 3x+y=1 \\
 & \Rightarrow y=-3x+1 \\
\end{align}$
This is the time when we should equate it with the equation of a line. It is y = mx + c where m is the point slope and c is the y intercept. After equating we come to know that m = - 3 and c = 1.
Hence, the point slope is – 3 and the y intercept is 1.

Note: To get through such questions, one should remember the standard equation of line, y intercept and the slope intercept. It was important to use both the formulas of $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ and $m=\dfrac{y-{{y}_{1}}}{x-{{x}_{1}}}$ because we have to include one ordered pair (x, y). This is why we were able to know the equation corresponding to the equation of line. We never use the equation of line to find x intercept. This is due to the fact that we have got y = mx + c and not x equals to any term. So, in case one might get confused about it thus, we should only consider y intercept always. Focus is also important to get the right answer otherwise we will lead towards the wrong answer.