
How do you graph
Answer
473.4k+ views
Hint: As we know that there are two kinds of intercepts which are
Complete step-by-step answer:
(i)
We are given the line equation:
As we are asked to draw the graph of
Now, as we know that
Therefore, the
(ii)
Similar to
Therefore, the
(iii)
Now, to draw a graph we need two points which lie on the line. As we have calculated both the intercepts, we can say that the line crosses the
Similarly, the line crosses the
Marking these two points on a graph and then joining the points through a line will give us the graphical representation of the line
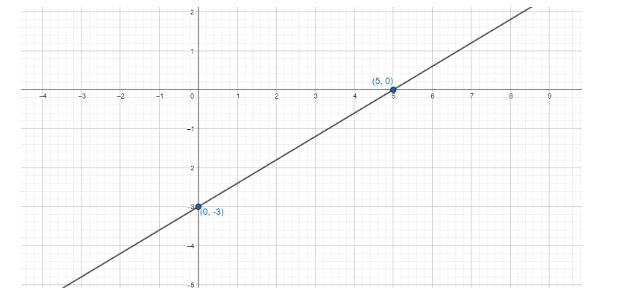
Hence, this is the line
Note: In an equation of the form
Complete step-by-step answer:
(i)
We are given the line equation:
As we are asked to draw the graph of
Now, as we know that
Therefore, the
(ii)
Similar to
Therefore, the
(iii)
Now, to draw a graph we need two points which lie on the line. As we have calculated both the intercepts, we can say that the line crosses the
Similarly, the line crosses the
Marking these two points on a graph and then joining the points through a line will give us the graphical representation of the line

Hence, this is the line
Note: In an equation of the form
Latest Vedantu courses for you
Grade 8 | CBSE | SCHOOL | English
Vedantu 8 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹45,300 per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




