
How do you graph, identify the domain, range, and asymptotes for
Answer
450.9k+ views
Hint: In order to graph the function given in the above question
Complete step-by-step answer:
The function to be graphed is given in the above question as
Since the function is a cosecant type function, we consider the graph of the cosecant function, which is written as
We know that its graph can be sketched as
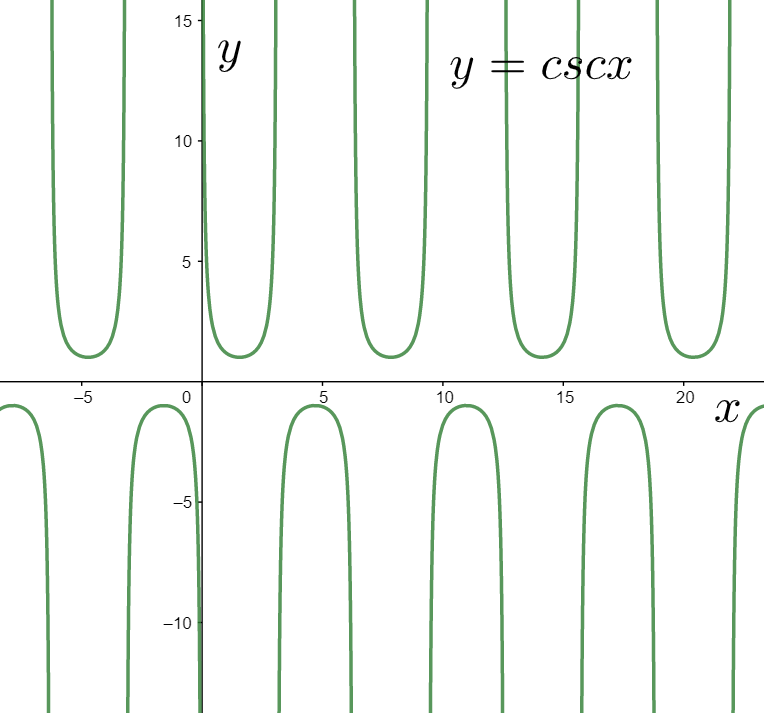
Now, we consider the graph of
It can be obtained by inverting the above graph with respect to the x axis as shown below.
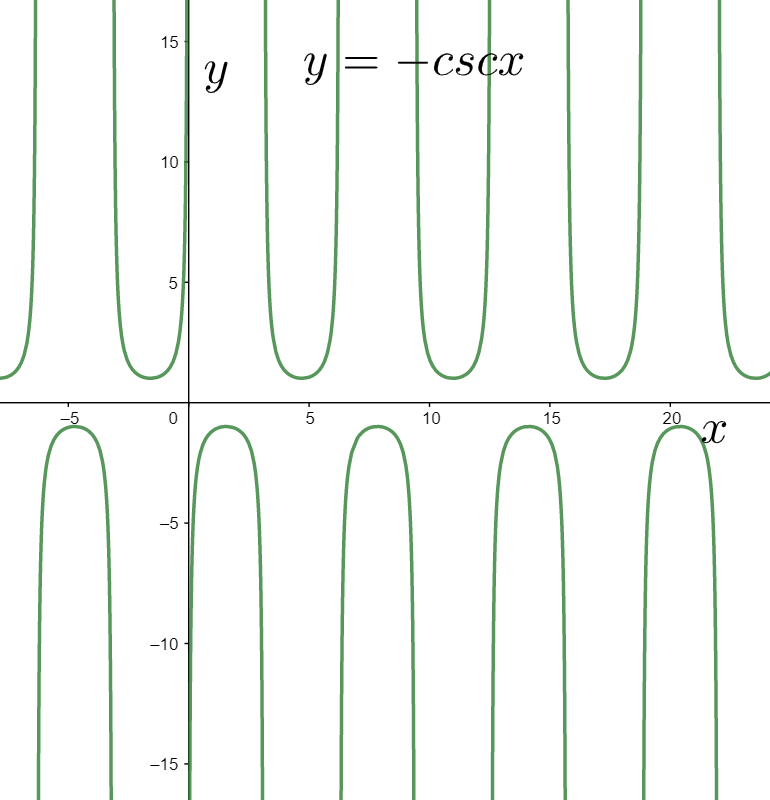
Now, we consider the graph of the function
It can be graphed by contracting the graph of the above function by two units in the vertical direction, as shown below.
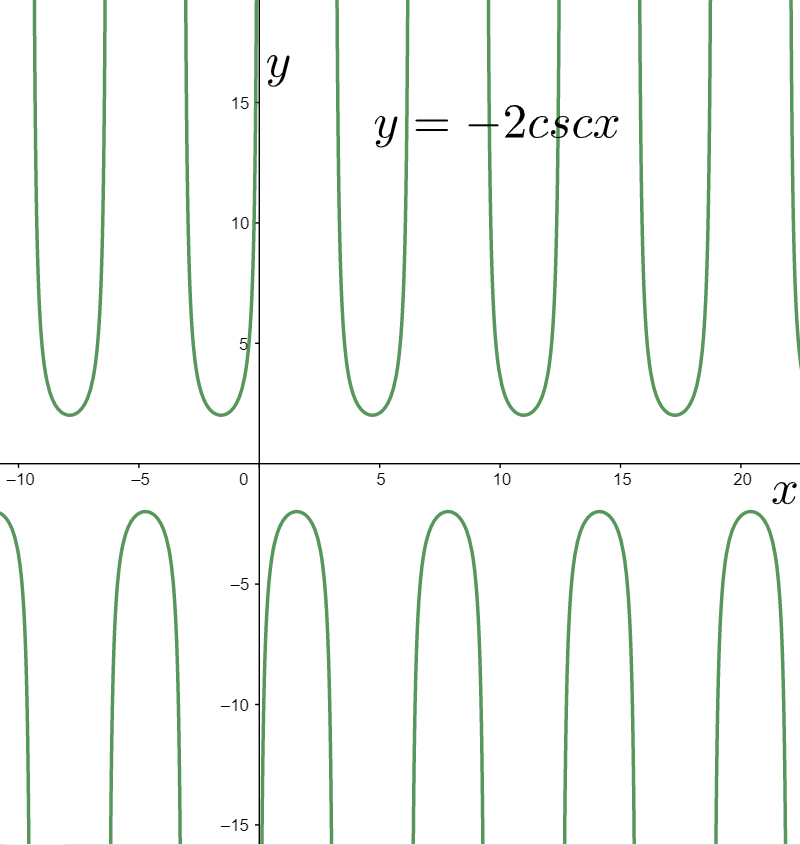
Now, we consider the graph of
For graphing it, we shift the above graph downwards by one unit in the vertical direction, as shown below.
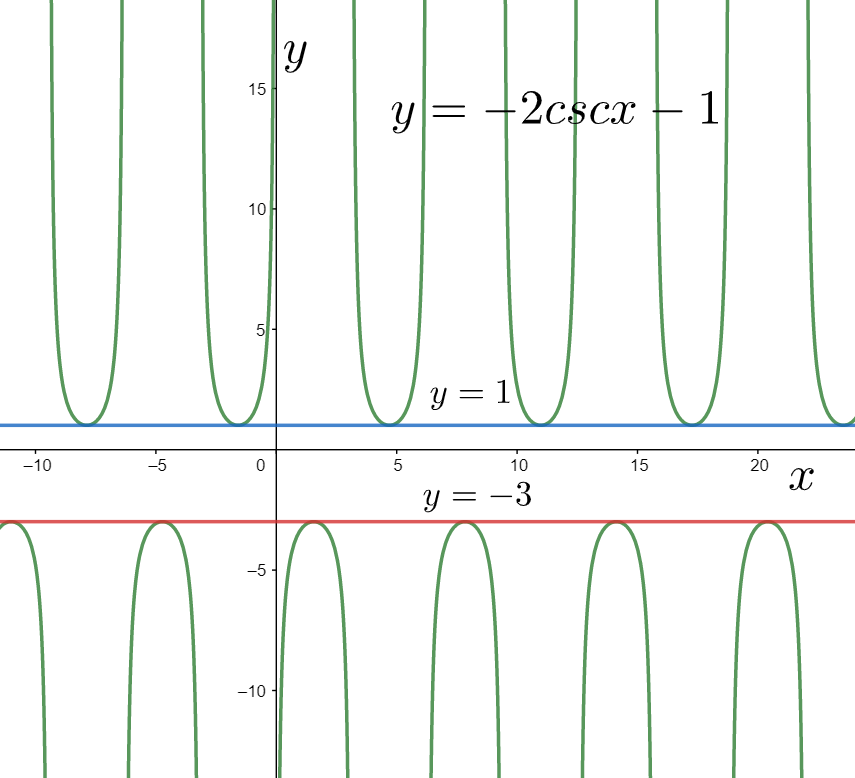
Finally, we consider the graph of the function
For graphing it, we contract the graph of the above function by two units in the horizontal direction as shown below.
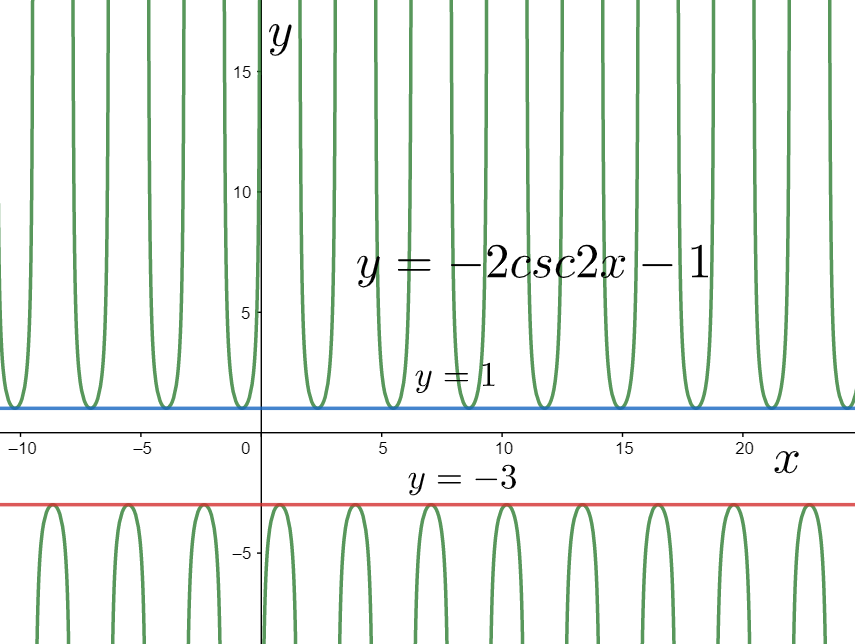
As we can see that the above graph starts from the line
Now, for obtaining the graph of the given function we started from the graph of the cosecant function
Also, the asymptotes are the lines about which the graph of the function approaches. We can see in the above graph that the asymptotes are the lines where the function is not defined, that is, at
Hence, we have identified the domain, range and the asymptotes for the given function.
Note: For solving these types of questions, we must be familiar with the concepts of the transformation of the graphs. We also must remember all the graphs of the basic trigonometric functions, since we need a basic graph to start with obtaining the geaph of a given trigonometric function from the transformation.
Complete step-by-step answer:
The function to be graphed is given in the above question as
Since the function is a cosecant type function, we consider the graph of the cosecant function, which is written as
We know that its graph can be sketched as

Now, we consider the graph of
It can be obtained by inverting the above graph with respect to the x axis as shown below.

Now, we consider the graph of the function
It can be graphed by contracting the graph of the above function by two units in the vertical direction, as shown below.

Now, we consider the graph of
For graphing it, we shift the above graph downwards by one unit in the vertical direction, as shown below.

Finally, we consider the graph of the function
For graphing it, we contract the graph of the above function by two units in the horizontal direction as shown below.

As we can see that the above graph starts from the line
Now, for obtaining the graph of the given function we started from the graph of the cosecant function
Also, the asymptotes are the lines about which the graph of the function approaches. We can see in the above graph that the asymptotes are the lines where the function is not defined, that is, at
Hence, we have identified the domain, range and the asymptotes for the given function.
Note: For solving these types of questions, we must be familiar with the concepts of the transformation of the graphs. We also must remember all the graphs of the basic trigonometric functions, since we need a basic graph to start with obtaining the geaph of a given trigonometric function from the transformation.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




