
How do you graph parametric equations?
Answer
448.5k+ views
Hint: The parametric equations are used to represent an implicit relation between the Cartesian variables x and y, each of which is explicitly expressed in terms of another variable, say t. Therefore, the parametric equations will always be a pair of equations, in which x and y variables are equated to some functions of t. For graphing the parametric equations, we need to eliminate the parameter t from the relations for x and y so as to obtain an explicit relation between these. We can take up the example of graphing the parametric equations given by
Complete step by step solution:
The parametric equations are the pair of equations in terms of a parameter t which represent an implicit relation between the variables x and y. Let us consider an example of the parametric equations given by
For graphing the parametric equations, we need to eliminate the parameter t so as to obtain an explicit relation between x and y. Therefore, considering the equation (i) we have
Adding
Substituting the above equation in the equation (ii) we get
The graph of the above equation can be shown as below.
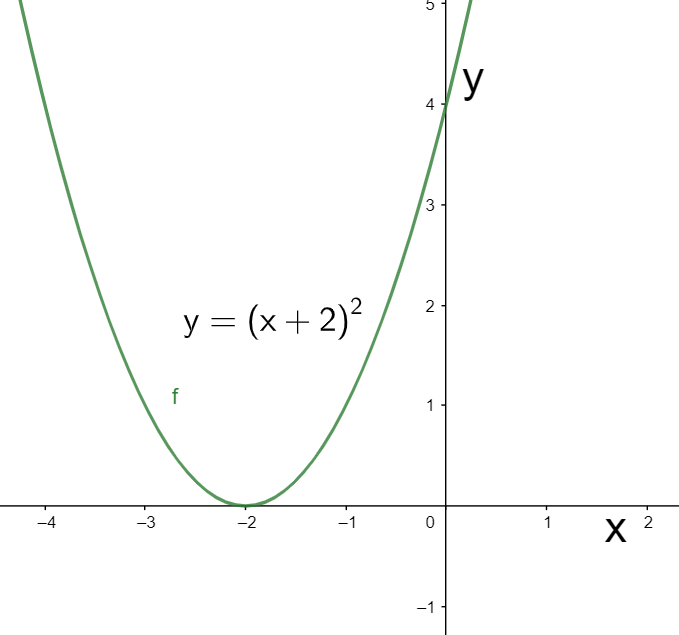
Hence, we have graphed the parametric equations
Note: The parametric equations, in some cases, may be unsolvable to obtain an explicit relation between x and y. In such cases, we are needed to make a table of values of x and y for the discrete values of t. But we must note that the graph obtained will not be smooth in such cases.
Complete step by step solution:
The parametric equations are the pair of equations in terms of a parameter t which represent an implicit relation between the variables x and y. Let us consider an example of the parametric equations given by
For graphing the parametric equations, we need to eliminate the parameter t so as to obtain an explicit relation between x and y. Therefore, considering the equation (i) we have
Adding
Substituting the above equation in the equation (ii) we get
The graph of the above equation can be shown as below.

Hence, we have graphed the parametric equations
Note: The parametric equations, in some cases, may be unsolvable to obtain an explicit relation between x and y. In such cases, we are needed to make a table of values of x and y for the discrete values of t. But we must note that the graph obtained will not be smooth in such cases.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




