Question

How do you graph the equation by plotting points $ y + 1 = 0 $ ?

Answer 1

Hint: To solve this question, compare the above given equation to the straight-line equation which is, $ y = mx + c $ and now write the value of the slope and y-intercept. Draw a graph by using the points which were found by comparing the equation. While drawing the graphs, take the correct units so that it looks clear.

Complete step by step solution:
Let us consider the given equation,
 $ y + 1 = 0 $
We know that the equation of the straight line is,
 $ y = mx + c $ , where $ m $ is the slope and $ c $ is the y-intercept
Now, rearrange the terms in the given equation regarding the straight-line equation we get,
 $ y = - 1 $
By looking at the above equation we come to know that it does not have any slope in the straight line and the value of y-intercept is $ - 1 $ , which literally means that when $ x = 0 $ , the value of $ y $ will be $ - 1 $ .
And the required point is $ (0, - 1) $ and the table for the graph is,

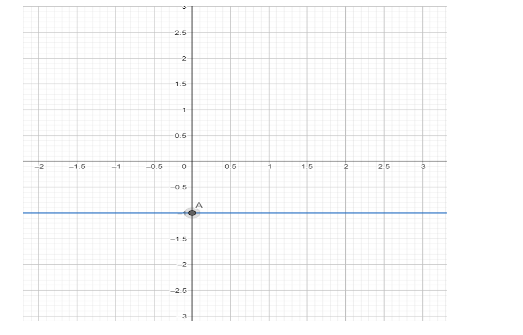
The blue line passing is the line whose equation has been given in the question and the point A, is the point out intersection at y-axis at -1 which forms the equation.
I have taken the unit as $ 1cm $ and the $ x - axis $ contains numbers from $ - 5 $ to $ 5 $ and repeated the same for $ y - axis $ also. This green line in the graph is the solution for the given equation. As the straight line is parallel to the axis, we cannot calculate the slope for the straight line.
This is the required solution.

Note: The line for the equation $ y + 1 = 0 $ is parallel to the $ x - axis $ , so there is no slope for this straight line. The slope or the gradient takes only when the equation of the straight line is perpendicular to the axes.