
How do you graph the lemniscate
Answer
451.5k+ views
Hint: We must first convert the given polar equation to the Cartesian equation by using the relations
Complete step-by-step solution:
The polar equation to be graphed is given in the above question as
We know that
Multiplying the above equation by
Now we know that the polar coordinates are related to the Cartesian coordinates as
Substituting the equations (ii), (iii) and (iv) into the equation (i) we get
Applying the algebraic identity
The above equation represents the Cartesian form of the given polar equation. For graphing it, we check the below points.
(i) Symmetry: We can see that the equation (v) contains the even powers of both x and y. Therefore, we can say that the curve will be symmetric with respect to both the x and y axes.
(ii) Intersection with the coordinate axes:
On substituting
Since on substituting
On substituting
Therefore, the curve cuts the x axis at
(iii) Tangent at origin: For this, we substitute the lowest degree term of equation (v) to zero. From the equation (v) we have
We can observe that the lowest degree in the above equation is equal to two. Equating the second degree term to zero, we get
Therefore, the tangents at the origin must be
Keeping in mind all of the above three points, we can graph the curve as below.
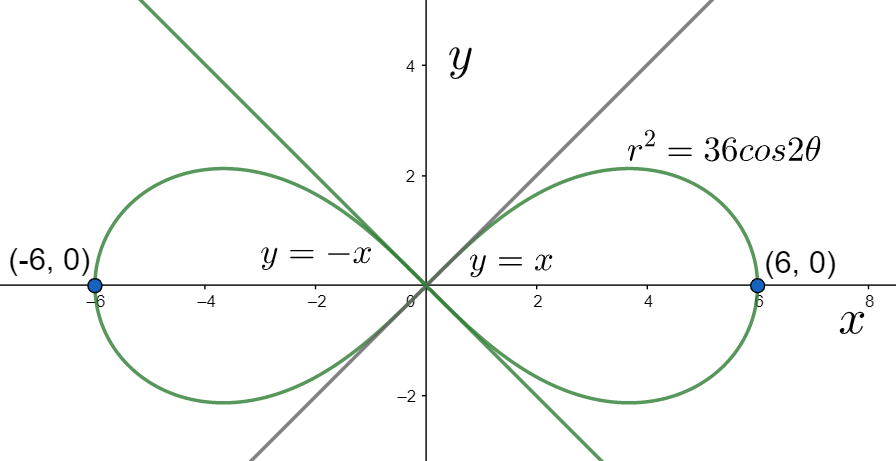
Hence, the given lemniscate has been graphed.
Note: Before finding the tangents at the origin, check whether the curve passes through the origin or not. This is because in the case if the curve does not pass through the origin, the tangent at origin will not exist. We must follow the order of the points as followed in the above solution, that is, symmetry, intersection with coordinate axis, and then tangents at origin.
Complete step-by-step solution:
The polar equation to be graphed is given in the above question as
We know that
Multiplying the above equation by
Now we know that the polar coordinates are related to the Cartesian coordinates as
Substituting the equations (ii), (iii) and (iv) into the equation (i) we get
Applying the algebraic identity
The above equation represents the Cartesian form of the given polar equation. For graphing it, we check the below points.
(i) Symmetry: We can see that the equation (v) contains the even powers of both x and y. Therefore, we can say that the curve will be symmetric with respect to both the x and y axes.
(ii) Intersection with the coordinate axes:
On substituting
Since on substituting
On substituting
Therefore, the curve cuts the x axis at
(iii) Tangent at origin: For this, we substitute the lowest degree term of equation (v) to zero. From the equation (v) we have
We can observe that the lowest degree in the above equation is equal to two. Equating the second degree term to zero, we get
Therefore, the tangents at the origin must be
Keeping in mind all of the above three points, we can graph the curve as below.

Hence, the given lemniscate has been graphed.
Note: Before finding the tangents at the origin, check whether the curve passes through the origin or not. This is because in the case if the curve does not pass through the origin, the tangent at origin will not exist. We must follow the order of the points as followed in the above solution, that is, symmetry, intersection with coordinate axis, and then tangents at origin.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




