Question

How do you graph the parabola \[y=2{{x}^{2}}-4x-6\]using vertex, intercept and additional points?

Answer 1

Hint: In this problem, we have the quadratic equation o \[y=2{{x}^{2}}-4x-6\], from which we have to draw the graph. To plot the points in the graph, we have to find the x-coordinate and y-coordinate of the vertex, x-intercept and y-intercept and some additional points to be plotted. We know that for x-intercept y=0 and for y-intercept, x=0, to find the x and y-intercept.

Complete step by step answer:
We know that the given quadratic equation is,
\[y=2{{x}^{2}}-4x-6\]…….. (1)
We also know that the standard form of the quadratic equation is,
\[y=a{{x}^{2}}+bx+c\]……… (2)
Now, we can compare the equation (1) and (2), we get
a = 2, b = -4, c = -6.
Now we have to find the vertex which is the maximum or minimum point of the parabola.
We know that, since a>0, the vertex is the minimum point and the parabola opens upwards.
Now, we can find the x-coordinate of the vertex, we also know the for the axis of symmetry,
\[x=\dfrac{-b}{2a}\]…… (3)
We can now substitute the value of a and b in (3), we get
\[\begin{align}
  & \Rightarrow x=\dfrac{-\left( -4 \right)}{2\left( 2 \right)} \\
 & \Rightarrow x=1 \\
\end{align}\]
Now, we can find the y-coordinate of the vertex by substituting the value of x in equation (1), we get
\[\begin{align}
  & \Rightarrow y=2{{\left( 1 \right)}^{2}}-4\left( 1 \right)-6 \\
 & \Rightarrow y=-8 \\
\end{align}\]
Therefore, the vertex is \[\left( 1,-8 \right)\]
Now, we have to find the x and y-intercept.
We know that, for y-intercept x=0, from equation (1),
\[\begin{align}
  & \Rightarrow y=2{{\left( 0 \right)}^{2}}-4\left( 0 \right)-6 \\
 & \Rightarrow y=-6 \\
\end{align}\]
Therefore, the y-intercept is \[\left( 0,-6 \right)\]
 Now, we have to find the x-intercept, where y=0, from (1) we get
\[\Rightarrow 2{{x}^{2}}-4x-6=0\]
By factoring this above equation, we get
\[\begin{align}
  & \Rightarrow 2\left( x+1 \right)\left( x-3 \right) \\
 & \Rightarrow x=\left( -1,3 \right) \\
\end{align}\]
The x-intercepts are \[\left( -1,0 \right),\left( 3,0 \right)\].
Now we can find the additional points by choosing value for x and y,
When x=2, then the value of y is,
\[\begin{align}
  & \Rightarrow y=2{{\left( 2 \right)}^{2}}-4\left( 2 \right)-6 \\
 & \Rightarrow y=8-8-6 \\
 & \Rightarrow y=-6 \\
\end{align}\]
One of the points is \[\left( 2,-6 \right)\]
We can find another point for x = -2, then y is,
\[\begin{align}
  & \Rightarrow y=2{{\left( -2 \right)}^{2}}-4\left( -2 \right)-6 \\
 & \Rightarrow y=8+8-6 \\
 & \Rightarrow y=10 \\
\end{align}\]
The other point is \[\left( -2,10 \right)\]
When x=4, the value of y is,
\[\begin{align}
  & \Rightarrow y=2{{\left( 4 \right)}^{2}}-4\left( 4 \right)-6 \\
 & \Rightarrow y=10 \\
\end{align}\]
Therefore, the third point is \[\left( 4,10 \right)\]
Now we can plot the vertex\[\left( 1,-8 \right)\], x-intercepts\[\left( -1,0 \right),\left( 3,0 \right)\], y-intercept\[\left( 0,-6 \right)\] and
 other points\[\left( 2,-6 \right)\],\[\left( -2,10 \right)\], \[\left( 4,10 \right)\]

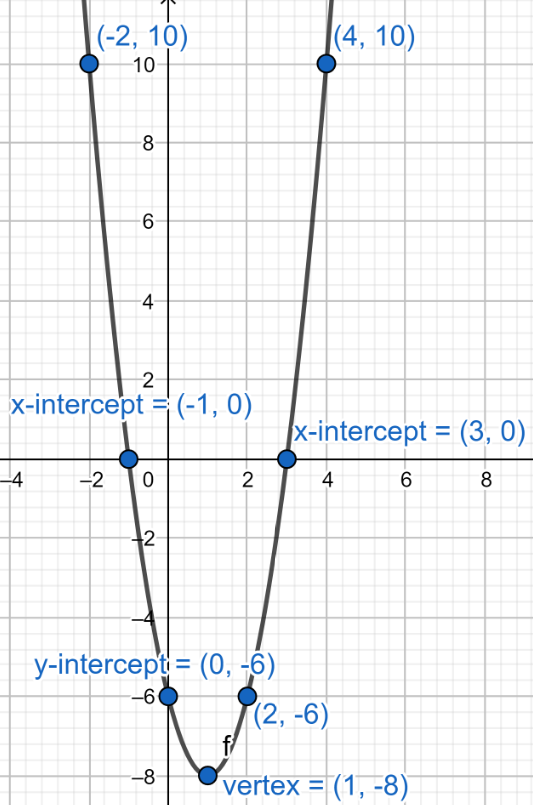
Note: Students may make mistakes in finding the value of vertex, it is done by using the axis symmetry formula of the parabola. Students should know some basic parabolic formulas to solve these types of problems. Students should remember that at x-intercept the value of y is 0 and at y-intercept the value of x is 0.