Question

Where will the hand of a clock stop if it starts at \[2\] and makes \[\dfrac{1}{2}\] of a revolution, clockwise?

Answer 1

Hint: We will use the property of the clock that the hand of a clock revolves at a complete angle of \[{360^\circ}\]which makes a complete clockwise revolution.

Complete step-by-step solution:
Step 1: To solve this problem, first we will make a clock as shown below:

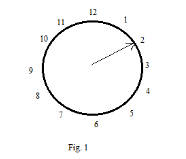
In fig (1), the hand of the clock is at \[2\]. Now we know in complete clockwise revolution, the hand of the clock makes an angle of \[{360^\circ}\]. That means the hand of the clock will start from \[2\] and after making revolution it will again end at \[2\].
But as per the question, the hand of the clock revolves \[\dfrac{1}{2}\] clockwise.
Step 2: If the hand of the clock making half revolution then the angle form by it will be half of the \[{360^\circ}\] as shown below:
\[{\text{Angle}} = \dfrac{{{{360}^\circ}}}{2} \Rightarrow {180^\circ}\]
Step 3: Now, by drawing an angle \[{180^\circ}\], we can find out that the hand of the clock stops at which point as shown in the below diagram:

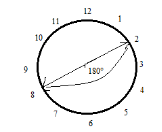
So, we can see from figure (2), that the hand of the clock makes an angle of \[{180^\circ}\] with the point \[8\].

The hand of the clock will stop at the point \[8\].

Note: Students should remember that the hand of the clock always revolves in the clockwise direction by making a complete revolution with an angle of \[{360^\circ}\].
We can also solve this question by the below method:
As we know that there are total \[12\] symbols in the clock in which the hand of the clock revolves itself.
Now, for making a complete clockwise revolution the hand of the clock will cover all these points and will come back again at the point \[2\].
But as per the question, it is only making half a revolution so if the hand of the clock is starting from a point \[2\], then it will cover \[6\] symbols in the clock which means \[2 + 6 = 8\]. So, the answer is \[8\].