Question

What happens when the $a$ (amplitude) of a sine graph is negative $-2\sin \left( \dfrac{1}{4}x \right)$?

Answer 1

Hint: To find out what happens when the amplitude of the graph is negative we will use the wave function. Firstly we will compare the given function by the general form of wave function and find out our amplitude then we will put the value of amplitude in the function with and without the negative sign. Finally we will let the value of $x=\pi $ and plot the values obtained and see what happens.

Complete step by step solution:
The function is given as below:
$y=-2\sin \left( \dfrac{1}{4}x \right)$…….$\left( 1 \right)$
The general form of wave equation is given as below:
$y=a\sin \left( bx+c \right)+d$……$\left( 2 \right)$
Where, $a=$ amplitude
On comparing equation (1) and (2) we get,
$a=-2$
So our negative amplitude is -2.
Let the positive amplitude be 2.
Now, Let $x=\pi $
Substituting $a=2$ and $x=\pi $ in equation (1) and solve to get,
$\begin{align}
  & y=2\sin \left( \dfrac{1}{4}\times \pi \right) \\
 & \Rightarrow y=2\sin \left( \dfrac{\pi }{4} \right) \\
 & \Rightarrow y=2\times \dfrac{1}{\sqrt{2}} \\
 & \therefore y=\sqrt{2} \\
\end{align}$

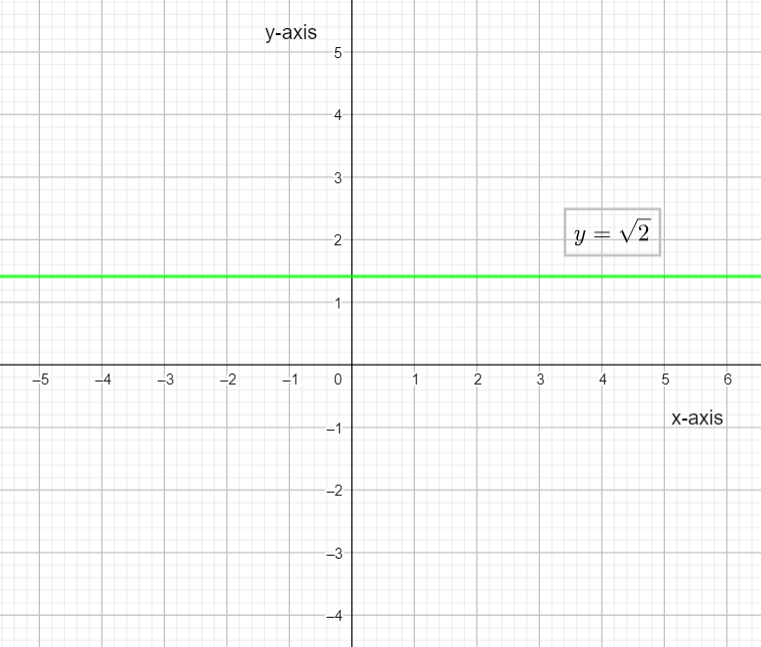
Substituting $a=-2$ and $x=\pi $ in equation (1) and solve to get,
$\begin{align}
  & y=-2\sin \left( \dfrac{1}{4}\times \pi \right) \\
 & \Rightarrow y=-2\sin \left( \dfrac{\pi }{4} \right) \\
 & \Rightarrow y=-2\times \dfrac{1}{\sqrt{2}} \\
 & \therefore y=-\sqrt{2} \\
\end{align}$

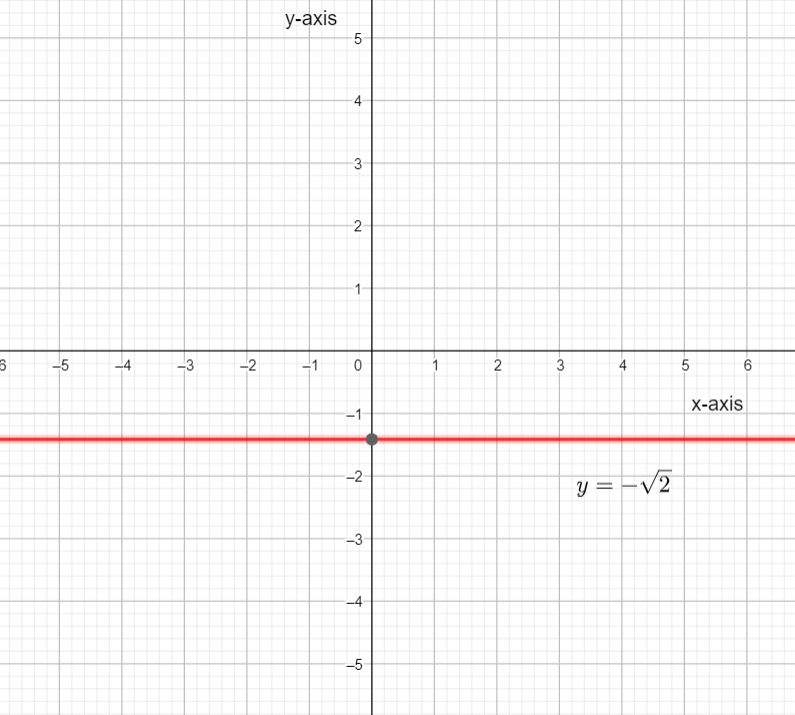
We can see from both the graphs that when we use negative amplitude the graph flip upside-down.
Hence the graph flips upside-down when the amplitude is negative.

Note: Amplitude is used to measure the change in a single period of a periodic function. Amplitude can also be expressed as height from the center line to the peak of the function whether the peak is above or below the line. Periodic functions are those who repeat forever and period is the distance between the two peaks of the graph. Amplitude of a sine function is the peak deviation of the function from zero.