Question

$\hat i$ and $\hat j$ are unit vectors along $x - axis$ and $y - axis$ respectively.
A) What is the magnitude and direction of the vectors $\left( {\hat i + \hat j} \right)$ and $\left( {\hat i - \hat j} \right)$ ?
B) What are the components of the vectors $\overrightarrow B = 2\hat i + 3\hat j$ along the direction of $\left( {\hat i + \hat j} \right)$ and $\left( {\hat i - \hat j} \right)$ ?

Answer 1

Hint:Use the value of $\hat i$ and $\hat j$ as $1$ because they are unit vectors. Now, to find the direction, find the inverse of $\tan $.
For finding the component of vectors find the angle between the vectors $\vec B$ and $\left( {\hat i + \hat j} \right)$ and then find the product of the angle and vector $\vec B$.

Complete step by step answer:
According to the question, we know that $\hat i$ and $\hat j$ are unit vectors along $x - axis$ and $y - axis$ respectively.
(a)
For finding the magnitude we use the expression –
$\vec A = \sqrt {{a^2} + {b^2} + {c^2}} $
Therefore, for calculating the magnitude of vector $\left( {\hat i + \hat j} \right)$ -
$ \Rightarrow \sqrt {{{\left( {\hat i} \right)}^2} + {{\left( {\hat j} \right)}^2}} $
We know that, $\hat i.\hat i = 1$ and $\hat j.\hat j = 1$
Therefore, magnitude of vector $\left( {\hat i + \hat j} \right)$ -
$ \Rightarrow \sqrt {{{\left( 1 \right)}^2} + {{\left( 1 \right)}^2}} = \sqrt 2 $
Hence, the magnitude of the vector $\left( {\hat i + \hat j} \right)$ is $\sqrt 2 $.

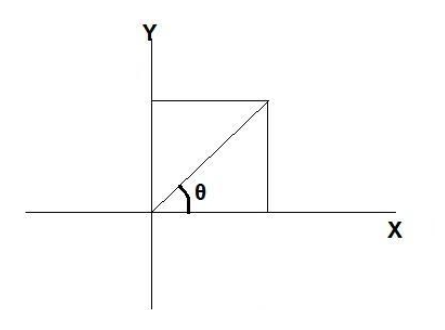
Now,
 $
  \tan \theta = \dfrac{1}{1} \\
  \theta = {\tan ^{ - 1}}\left( 1 \right) \\
  \theta = {45^ \circ } \\
 $
Therefore, the direction is ${45^ \circ }$ to the $x - axis$.
Now, calculating the magnitude of vector $\left( {\hat i - \hat j} \right)$ -
$ \Rightarrow \sqrt {{{\left( 1 \right)}^2} + {{\left( { - 1} \right)}^2}} = \sqrt 2 $

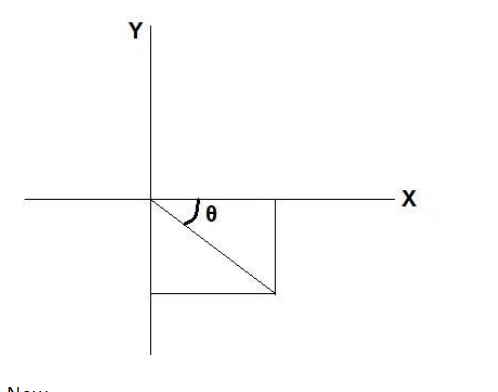
Now,
$
  \tan \theta = - \dfrac{1}{1} \\
  \theta = {\tan ^{ - 1}}\left( { - 1} \right) \\
  \theta = - {45^ \circ } \\
 $
Hence, the direction of the vector $\left( {\hat i - \hat j} \right)$ is $ - {45^ \circ }$ with the $x - axis$.

(b)
From the question, it is given that –
$\overrightarrow B = 2\hat i + 3\hat j$
Let,
$
  \vec a = \hat i + \hat j \\
  \vec b = \hat i - \hat j \\
 $
To get the component of $\vec B$ along the direction of $\vec a$ we have to find the angle between them –
So, we need to do this by their dot product –
$
  \vec B.\vec a = \left| {\vec B} \right|\left| {\vec a} \right|\cos \theta \\
  \cos \theta = \dfrac{{\vec B.\vec a}}{{\left| {\vec B} \right|\left| {\vec a} \right|}} \cdots \left( 1 \right) \\
 $
Magnitude of vector $\vec B$ -
$\left| {\vec B} \right| = \sqrt {{{\left( 2 \right)}^2} + {{\left( 3 \right)}^2}} = \sqrt {4 + 9} = \sqrt {13} units$
Magnitude of vector $\vec a$ -
$\left| {\vec a} \right| = \sqrt {1 + 1} = \sqrt 2 $
Putting all the values needed for finding the component in equation $\left( 1 \right)$, we get –
$
  \therefore \cos \theta = \dfrac{{\left( {2\hat i + 3\hat j} \right).\left( {\hat i + \hat j} \right)}}{{\sqrt {13} \times \sqrt 2 }} = \dfrac{{2 + 3}}{{\sqrt {26} }} \\
  \cos \theta = \dfrac{5}{{\sqrt {26} }} \\
 $
Hence, the component of $\vec B$ along direction of $\vec a$ is $\dfrac{5}{{\sqrt {26} }}\left( {2\hat i + 3\hat j} \right)$
Similarly,
To get the component of $\vec B$ along the direction of $\vec b$ we have to find the angle between them –
So, we need to do this by their dot product –
$
  \vec B.\vec b = \left| {\vec B} \right|\left| {\vec b} \right|\cos \theta \\
  \cos \theta = \dfrac{{\vec B.\vec b}}{{\left| {\vec B} \right|\left| {\vec b} \right|}} \cdots \left( 2 \right) \\
 $
Magnitude of vector $\vec b$ -
$\left| {\vec b} \right| = \sqrt {1 + 1} = \sqrt 2 $
Putting all the values needed for finding the component in equation $\left( 2 \right)$, we get –
$
  \therefore \cos \theta = \dfrac{{\left( {2\hat i + 3\hat j} \right).\left( {\hat i - \hat j} \right)}}{{\sqrt {13} \times \sqrt 2 }} = \dfrac{{2 - 3}}{{\sqrt {26} }} \\
  \cos \theta = \dfrac{{ - 1}}{{\sqrt {26} }} \\
 $
Hence, the component of $\vec B$ along direction of $\vec a$ is $\dfrac{{ - 1}}{{\sqrt {26} }}\left( {2\hat i + 3\hat j} \right)$.

Note: -The magnitude of a vector is the length of the vector. The magnitude of the vector $\vec a$ is denoted as $\left| {\vec a} \right|$.
Formulas for the magnitude of vectors in two dimensions in terms of their coordinates are –
If $\vec a = {a_1}\hat i + {a_2}\hat j$ then, magnitude is –
$\left| {\vec a} \right| = \sqrt {a_1^2 + a_2^2} $