
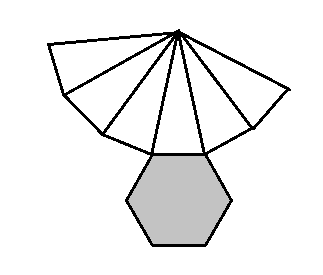
Hexagonal pyramid is
A)True
B)False

Answer
381.9k+ views
Hint: In this problem, we have to find the given problem is true or false. That which the given hexagonal pyramid is
Complete step y step answer:
In the picture, the base is hexagonal which has six sides.
The pyramid will have one additional triangular face. That for each edge of the base. This makes that the total of seven faces.
That is six triangular faces plus one hexagonal face in the given picture.
The base provides the six vertices and the top of the pyramid gives one more vertex.
Therefore for the picture, there are a total of seven vertices.
There are twelve edges in the given picture.
Six edges are made by the base.
And the other six edges are shared edges extending.
Therefore totally there are twelve edges.
Therefore the solution for this question is true.
We can write this explanation as mathematical terms like,
Number of faces in the net
Number of vertices in the net
Number of edges in the net
Therefore the possible shape we get from the net is the hexagonal pyramid.
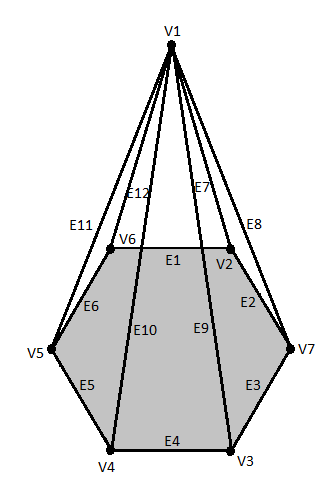
Therefore the solution for the given question is option A true.
The explanation for the option B: Option B is false.
From the above solution, we explain why the answer is true.
Therefore option B is not an answer for the given question.
Note:
In mathematics, a hexagonal pyramid is defined as a pyramid with a hexagon base. Vertices are defined as the point where the two lines meet and form an angle and the corners. Simply defined as the face is a flat surface. And a vertex is the corner where the edges are meeting.
Complete step y step answer:
In the picture, the base is hexagonal which has six sides.
The pyramid will have one additional triangular face. That for each edge of the base. This makes that the total of seven faces.
That is six triangular faces plus one hexagonal face in the given picture.
The base provides the six vertices and the top of the pyramid gives one more vertex.
Therefore for the picture, there are a total of seven vertices.
There are twelve edges in the given picture.
Six edges are made by the base.
And the other six edges are shared edges extending.
Therefore totally there are twelve edges.
Therefore the solution for this question is true.
We can write this explanation as mathematical terms like,
Number of faces in the net
Number of vertices in the net
Number of edges in the net
Therefore the possible shape we get from the net is the hexagonal pyramid.

Therefore the solution for the given question is option A true.
The explanation for the option B: Option B is false.
From the above solution, we explain why the answer is true.
Therefore option B is not an answer for the given question.
Note:
In mathematics, a hexagonal pyramid is defined as a pyramid with a hexagon base. Vertices are defined as the point where the two lines meet and form an angle and the corners. Simply defined as the face is a flat surface. And a vertex is the corner where the edges are meeting.
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
School Full course for MAHARASHTRABOARD students
₹33,300 per year
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE




