Question

How many hours would make a day if the Earth were rotating at such a high speed that the weight of a body on the equator was zero?
$\begin{align}
  & A.6.2h \\
 & B.1.4h \\
 & C.28h \\
 & D.5.6h \\
\end{align}$

Answer 1

Hint: The weight of the body is not only due to the gravitational force of the earth. It is also affected by centrifugal force acting on a body due to the rotation of the earth. Find out the value of the centrifugal acceleration of the body at the equator and hence find out the effective acceleration. Using this expression, find out the effective weight of the body at the equator. Assuming the weight of the body at the equator is zero, obtain an expression for the angular velocity of the earth in terms of the radius of the earth and acceleration due to gravity. Now calculate the period of rotation of the earth which is nothing but the duration of the day.

Formula Used:
The effective weight of the body,
$m{{g}_{eff}}=mg-mR{{\omega }^{2}}\cos \lambda $
Where,
m is the mass of the body
g is the true acceleration due to gravity
R is the radius of the Earth
\[\lambda\] is the latitude
\[\omega \] is the angular velocity of the Earth
Period of rotation,
$T=\dfrac{2\pi }{\omega }$

Complete step-by-step answer:

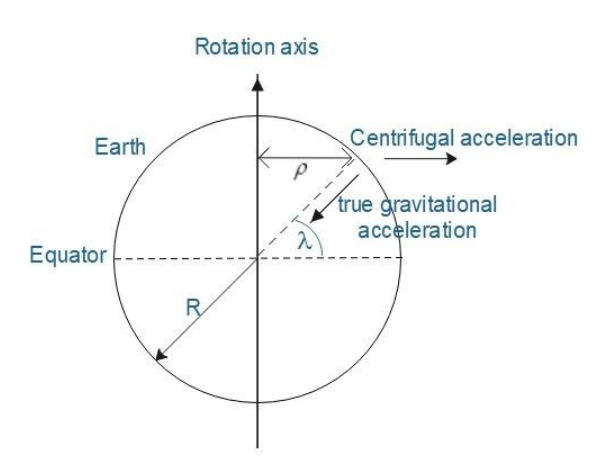
A day is a time taken by the planet to complete one full rotation about its axis of rotation. It depends on the angular velocity of the planet. More the angular velocity, shorter will be the day. Thus, one day on a planet is nothing but the period of rotation of that planet. Hence, one day on the earth is equal to the period of rotation of the Earth.
Let \[\omega \] be the angular velocity of the Earth. Then the period of rotation of the Earth is
$T=\dfrac{2\pi }{\omega }$
Due to the rotation of the earth, a centrifugal force acts on everybody on earth and its value depends on the position of the body on the Earth. The value of centrifugal force changes with latitude. It is maximum at the equator.
Thus as you can see in the diagram if $\lambda $ is the latitude of the body on earth then the centrifugal force acting on the body is given by
${{F}_{CF}}=mR{{\omega }^{2}}\cos \lambda $ …………………………. (i)
As force F is the product of the mass of the body m and its acceleration a, the centrifugal force can also be given as
${{F}_{CF}}=m{{g}_{CF}}$ ……………………………… (ii)
Where ${{g}_{CF}}$ is the centripetal acceleration of the body.
Comparing equation (i) and (ii), we get,
${{g}_{CF}}=R{{\omega }^{2}}\cos \lambda $
If g is acceleration due gravity at the equator then the effective acceleration due to gravity is given as
$\begin{align}
  & {{g}_{eff}}=g-{{g}_{CF}} \\
 & {{g}_{eff}}=g-R{{\omega }^{2}}\cos \lambda \\
\end{align}$
The weight of the body is just the gravitational force acting on that body. Thus, on the surface of the earth, effective weight of the body is
$m{{g}_{eff}}=mg-mR{{\omega }^{2}}\cos \lambda $
At the equator, $\lambda =0$. Therefore, $\cos \lambda =1$
Thus, the weight of the body at equator is
$m{{g}_{eff}}=mg-mR{{\omega }^{2}}$
If weight of the body at equator is zero then,
$\begin{align}
  & 0=mg-mR{{\omega }^{2}} \\
 & \therefore mg=mR{{\omega }^{2}} \\
 & \Rightarrow \omega =\sqrt{\dfrac{g}{R}} \\
\end{align}$
Thus, the period of rotation of the earth will be given by:
$\begin{align}
  & T=\dfrac{2\pi }{\sqrt{\dfrac{g}{R}}} \\
 & T=2\pi \sqrt{\dfrac{R}{g}} \\
\end{align}$
For Earth,
$R=6400km=6.4\times {{10}^{6}}m$ and $g=9.8m{{s}^{-2}}$
Thus,
$\begin{align}
  & T=2\times 3.124\times \sqrt{\dfrac{6.4\times {{10}^{6}}}{9.8}}=5078\sec \\
 & T=\dfrac{5078}{60\times 60}h \\
 & T\approx 1.4h \\
\end{align}$
Therefore, one day on the Earth would be 1.4h if the Earth is rotating at such a high speed that the weight of a body on the equator was zero.
Hence the correct answer is option B.

Note: When the body is in the rotating system then pseudo forces act on it. One of the pseudo forces is the centrifugal force. The centrifugal force acts in such a way that it throws away the body in a direction tangent to the rotating path. The effect of centrifugal force is maximum along the equator of the earth and minimum at the poles.