Question

How can planes intersect?

Answer 1

Hint: There are three ways that two planes can intersect.
Two planes do not intersect if they are parallel.
Two planes do not intersect if they are in a line.
Two planes do not intersect if they are coincident.

Complete step-by-step answer:
Let us understand three ways that two planes can intersect.
In three dimensional Euclidean space,
Let us take the first condition, where two planes do not intersect if they are parallel.
If two planes are identical to the other except translated by some vector, not in the plane, then the two planes do not intersect, then they are parallel.

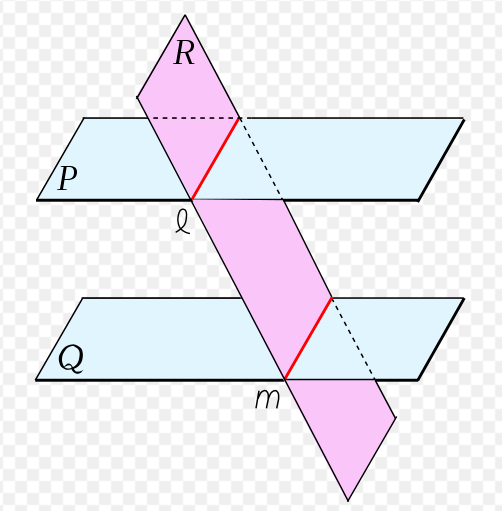
Now, take the second condition, where two planes do not intersect if they are in a line.
Since the equation of a plane consists of three variables and two equations of planes are given. And by solving the equations, we will get the relation between the three variables that is equivalent to the equation of the intersection line. Two planes cannot intersect in one or a finite number of points.

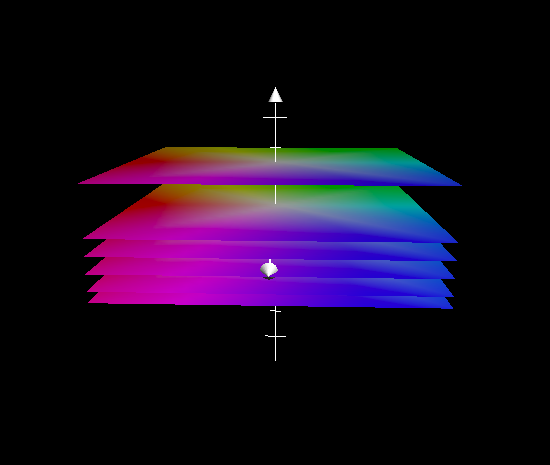
Let us take the third condition, where two planes do not intersect if they are coincident.
Two planes are coincident when they have the same or parallel normal vectors and their equations are scalar multiples of each other.

Note:
Plane: It is a flat, two-dimensional surface that extends infinitely far. It is the two dimensional analogue of a point, a line, and three-dimensional space. Many fundamental tasks in mathematics, geometry, trigonometry, graph theory, and graphing are performed in a two-dimensional plane.