Question

How do you bisect an obtuse angle?

Answer 1

Hint: An angle bisector is a line that divides an angle into two halves. Any angle, including obtuse angle, can be bisected by constructing congruent triangles with the common side-lying on an angle’s bisector. It can be an acute angle or an obtuse angle or a right angle. The type of angle makes no difference in the process of bisection.

Complete step by step answer:
Suppose an obtuse angle to be bisected be \[\angle ABC\] with vertex \[B\] and two sides \[BA\] and \[BC\] as shown in the figure below.

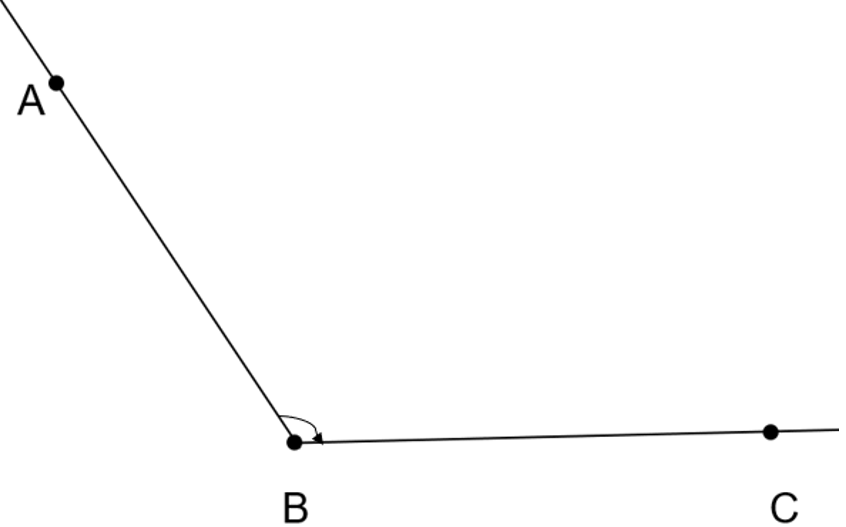
We choose any segment of some length \[d\] and mark point \[M\] on side \[BA\] on a distance \[d\] from vertex \[B\].
Using the same segment of length \[d\], we mark point \[N\] on side \[BC\] on distance \[d\] from vertex \[B\].
This is shown in the figure below.

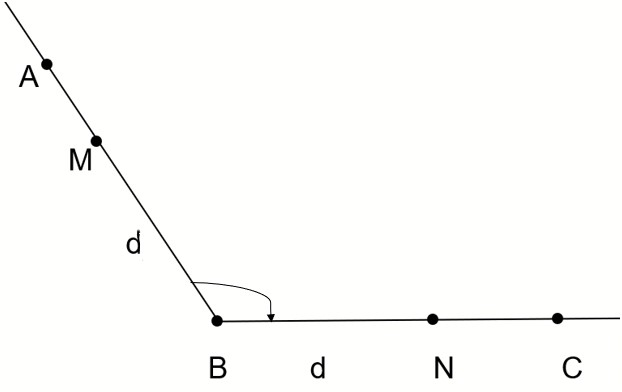
We can now say that \[BM\cong BN\].

We choose a radius sufficiently large (greater than half the distance between points \[M\] and \[N\]) and then we draw two circles with centres at points \[M\] and \[N\] of this radius. These two circles intersect at two points, \[P\] and \[Q\].

Choosing any of these intersecting points, we have to connect it with vertex \[B\]. This line is the bisector of an obtuse angle \[\angle ABC\]. This process is shown in the figure below.

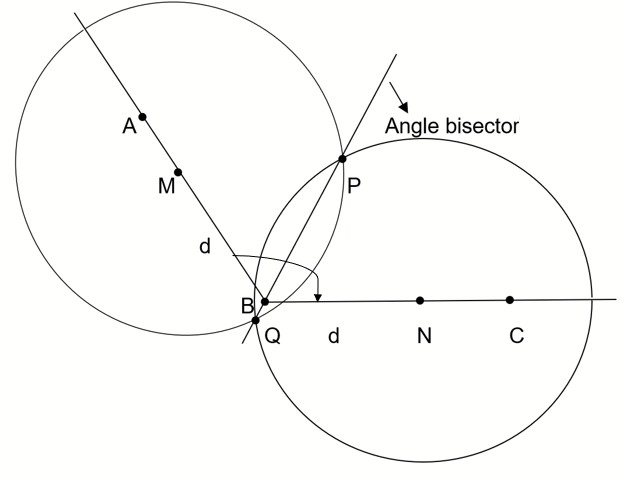
Proof: -

On comparing triangles \[\Delta BMP\] and \[\Delta BMP\], we can comment the following:
1. They share side BP.
2. \[BM\cong BN\] by construction, since we used the same length \[d\] to mark both points \[M\] and \[N\].
3. \[MP\cong NP\] by construction, since we used the same radius of two intersecting circles with centres at points \[M\] and \[N\].

\[\therefore \] Triangles \[\Delta BMP\] and \[\Delta BMP\] are congruent by three sides: \[~\Delta BMP\cong \Delta BNP\].
As a consequence of congruency, we can say that \[\angle MBP=\angle NBP\].

\[\, therefore, \] The line BP is the angle bisector of \[\angle ABC\].

Note:
 We can simply draw the angle bisector using a protractor. While constructing using the compass, we need to take care of the position of the center where we put one end of the compass. Silly mistakes are to be avoided in the whole process to get the correct answer.