
How do you derive the law of cosine?
Answer
465.9k+ views
Hint: the law of cosines implies the relation between the lengths of sides of a triangle with respect to the cosine of its angle.in a right angle triangle cosine of an angle is the length of the adjacent side divided by the length of the hypotenuse.to derive the law of cosine we will use trigonometric functions and their property. The trigonometry functions are the real functions which relate an angle of a right angled triangle to the ratio of two side lengths. We will use the Pythagorean Theorem to prove the law of cosine. The cosine is a periodic function having period of
According to cosine law,
If
Complete step by step answer:
Step: 1
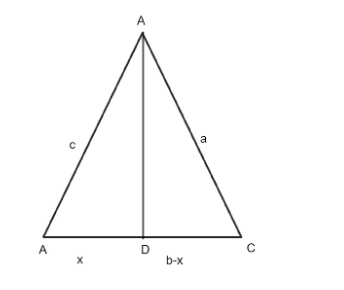
Consider the triangle ADB ,
Take cosine in the triangle ADB,
Step: 2 use Pythagoras theorem in the triangle ADB,
Use the Pythagoras theorem in the triangle CDB,
Substitute the value of
Substitute the value of
Note: Using the law of cosine we can find the unknown angle. If the angle between sides are equal to 90 then cosine rule will satisfy the Pythagoras theorem. Students are advised to draw the triangle and derive the law of cosine. They must use the cosine formula to prove the rule. They should know to apply Pythagoras theorem in the triangle. Students are advised to derive the rule of cosine step by step.
According to cosine law,
If
Complete step by step answer:
Step: 1

Consider the triangle ADB ,
Take cosine in the triangle ADB,
Step: 2 use Pythagoras theorem in the triangle ADB,
Use the Pythagoras theorem in the triangle CDB,
Substitute the value of
Substitute the value of
Note: Using the law of cosine we can find the unknown angle. If the angle between sides are equal to 90 then cosine rule will satisfy the Pythagoras theorem. Students are advised to draw the triangle and derive the law of cosine. They must use the cosine formula to prove the rule. They should know to apply Pythagoras theorem in the triangle. Students are advised to derive the rule of cosine step by step.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




