
How do you graph
Answer
474.9k+ views
Hint: The logarithm base b of a number n is the number x that when b is raised to
Complete step by step answer:
If we observe the given expression, we get to know that the base of this logarithmic function is
We can directly find the logarithmic graph by taking the image of a graph of an exponential function with respect to any of the lines
The below graph says that
In the below graph, first we draw a graph of
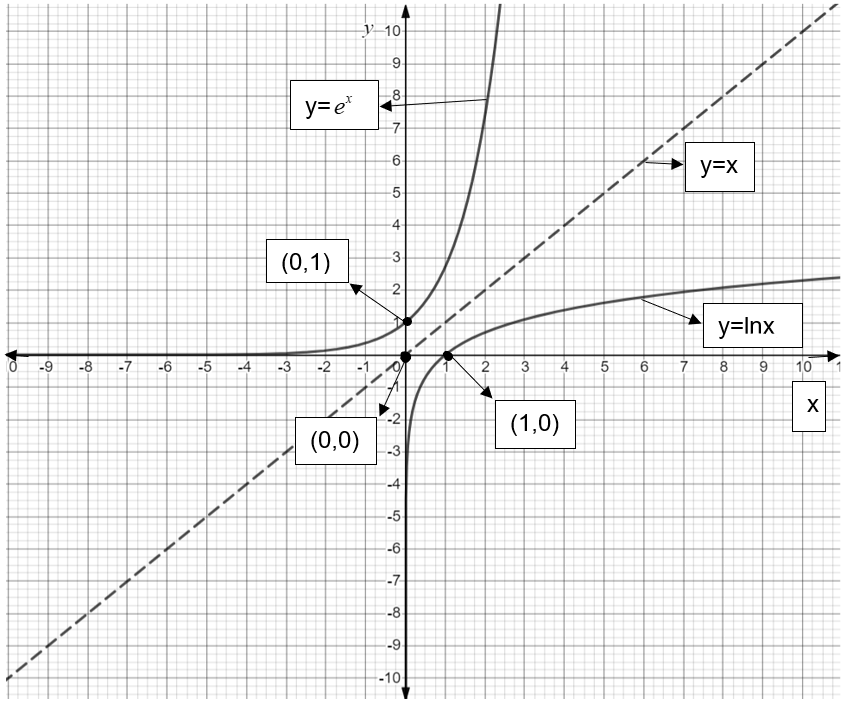
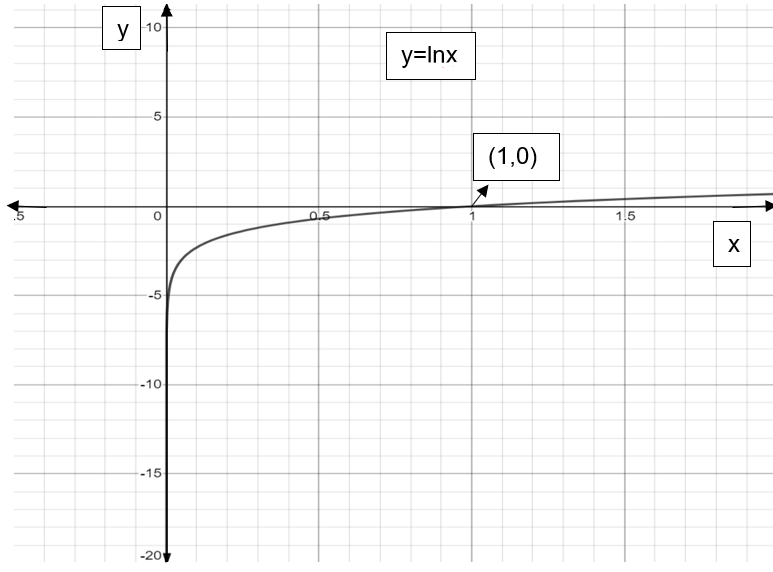
The graph of
Note:
We should be thorough with the logarithm and exponent concept to avoid mistakes like taking base 10 for
Complete step by step answer:
If we observe the given expression, we get to know that the base of this logarithmic function is
We can directly find the logarithmic graph by taking the image of a graph of an exponential function with respect to any of the lines
The below graph says that
In the below graph, first we draw a graph of

The graph of

Note:
We should be thorough with the logarithm and exponent concept to avoid mistakes like taking base 10 for
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
School Full course for MAHARASHTRABOARD students
₹33,300 per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the full form of POSCO class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

Discuss the main reasons for poverty in India




