
How do you graph the function y = logx?
Answer
473.1k+ views
Hint: In this question, we need to graph the function y = logx. Since no base is given so we will consider it as 10 and draw the graph for
Complete step by step answer:
Here we are given the function as y = logx. We need to plot a graph for this function. Here we are not given any base for logarithm so we will assume the base as 10 and draw the graph for
Let us first find the equation of the line of asymptote so that we properly graph our function running along the asymptote.
For finding asymptote we need to put the argument of the logarithm as zero (angle of the log). Here we have x = 0.
So equation of asymptote is x = 0.
Now let us find some points to plot.
For x = 1 we have
For x = 2 we have
For x = 10 we have
For
For
For
Our point table becomes
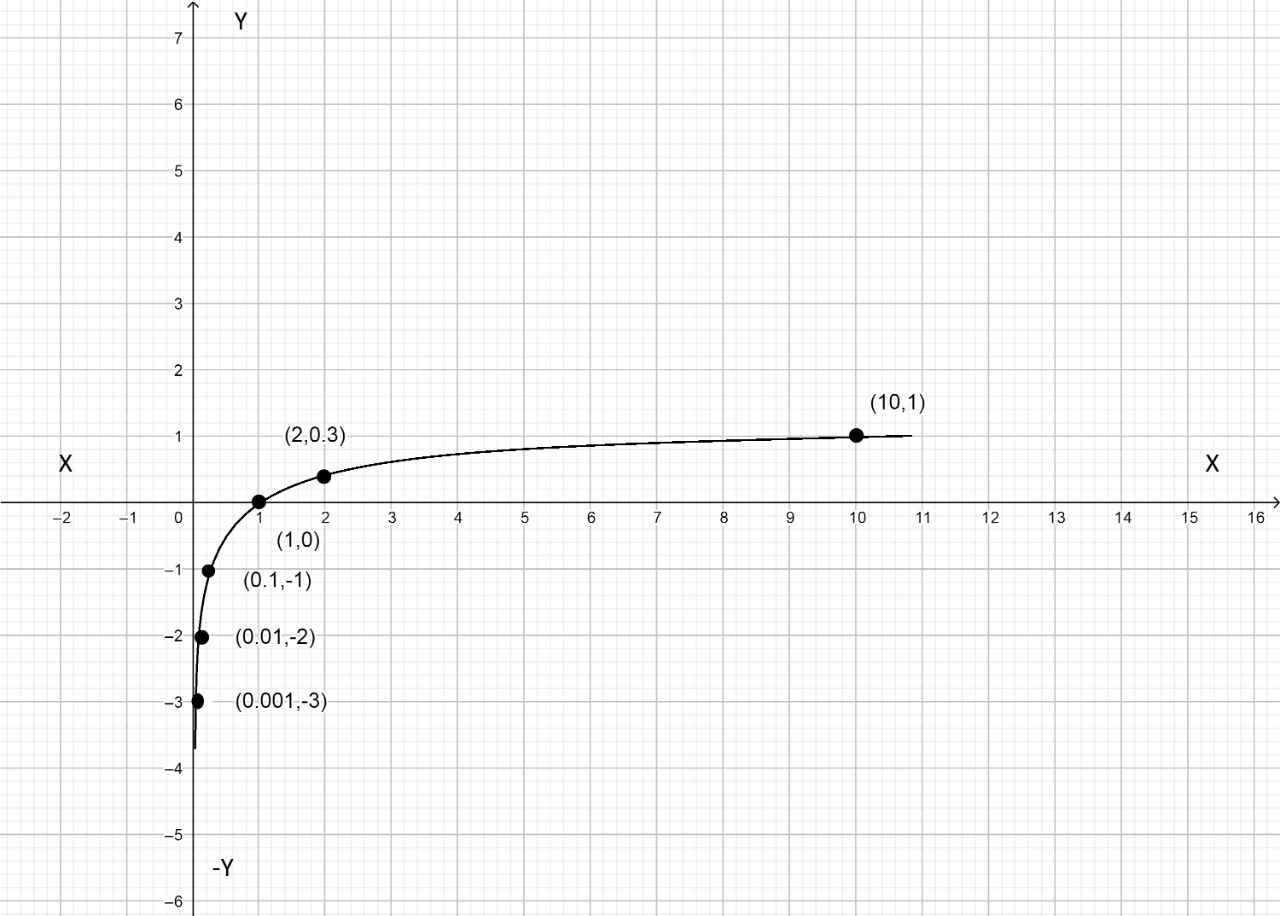
Plotting these points on the graph and taking care of asymptote our graph looks like this,
Note:
Students should note that x cannot be negative. Also, log0 does not exist. Take care while plotting the points on the graph. If the base of the logarithmic function is different our graph changes. The general shape remains the same.
Complete step by step answer:
Here we are given the function as y = logx. We need to plot a graph for this function. Here we are not given any base for logarithm so we will assume the base as 10 and draw the graph for
Let us first find the equation of the line of asymptote so that we properly graph our function running along the asymptote.
For finding asymptote we need to put the argument of the logarithm as zero (angle of the log). Here we have x = 0.
So equation of asymptote is x = 0.
Now let us find some points to plot.
For x = 1 we have
For x = 2 we have
For x = 10 we have
For
For
For
Our point table becomes
| x | 1 | 10 | |||
| y | -3 | -2 | -1 | 0 | 1 |
Plotting these points on the graph and taking care of asymptote our graph looks like this,

Note:
Students should note that x cannot be negative. Also, log0 does not exist. Take care while plotting the points on the graph. If the base of the logarithmic function is different our graph changes. The general shape remains the same.
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE




