Question

How do you graph \[x < - 2\]?

Answer 1

Hint: For two dimensional graph, sketch a line of the equation \[x = - 2\] which is parallel to y-axis with a dotted line, cut x-axis at negative of two and shade the region that belongs to the left of the dotted line.

Complete step by step solution:
Write the given linear inequality.
\[x < - 2\] …… (1)
To draw the graph of linear inequality \[x < - 2\] in a Cartesian plane first we have to assume that \[x\] is equal to \[ - 2\].
\[ \Rightarrow x = - 2\]
Now, draw the graph for a linear equation \[x = - 2\] in two dimension Cartesian plane by the use of knowledge that graph of \[x = a\] is a line parallel to the \[y\]-axis that crosses the \[x\]-axis at \[a\] in two dimension x-y planes.
Remember that the line must be dotted as the given inequality does not include an equality sign in this situation. So, all the points that pass through the line \[x = - 2\] are not the solution of \[x < - 2\].
It is observed that all the regions left to the dotted line \[x = - 2\] satisfy the solution for \[x < - 2\].
So, shade all the regions left to the dotted line of \[x = - 2\] which is the required solution or graph for the inequality \[x < - 2\].
The required graph for the linear inequality \[x < - 2\] is shown in figure 1 below.

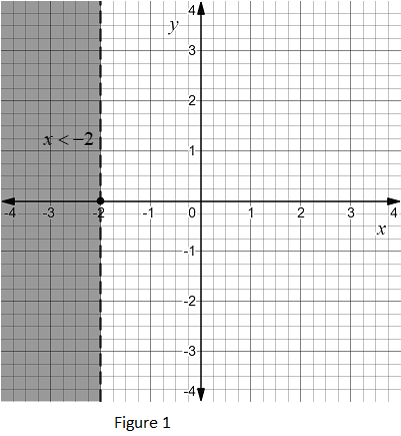
The figure 1 shows the graph of linear inequality \[x < - 2\] in two dimensions or a Cartesian plane.
We can also graph the inequality \[x < - 2\] in a real number line or one dimension as shown below.
In the real number line, locate the point \[x = - 2\] and represent this point as a hollow dot.
Then, all the points on the left of \[x = - 2\] are less than \[ - 2\].
So, dark the whole number line left to the hollow point \[ - 2\] as shown in Figure 2.

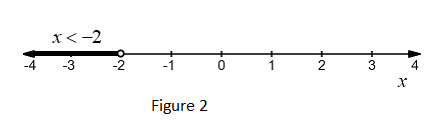
Thus, figure 1 and 2 show the graph of linear inequality in two dimensions and one dimension respectively.

Note: Solution of the linear inequality \[x < - 2\] form an area of shaded region in two dimensions but in one dimension it is a line.