
How do you graph
Answer
462.3k+ views
Hint:Change of form of the given equation will give the x-intercept and y-intercept of the line
Then we place the points on the axes and from there we draw the line on the graph.
Complete step by step solution:
We are taking the general equation of line to understand the slope and the intercept form of the line
We change from the equation
The given equation is in the form of
We have to find the x-intercept, and y-intercept of the line
For this we convert the given equation into the form of
The given equation is
we get
We don’t find any intercepts as the form is not possible to create. This means the line intersects the axes at the same point. We can see that the line goes through the origin of
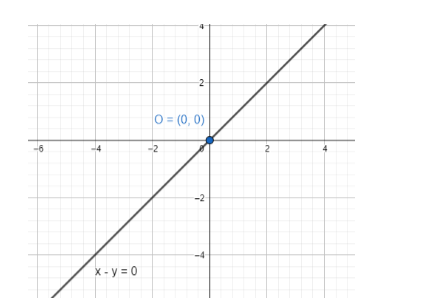
Note: A line parallel to the X-axis does not intersect the X-axis at any finite distance. Hence, we cannot get any finite x-intercept of such a line. Same goes for lines parallel to the Y-axis. In case of slope of a line the range of the slope is 0 to
Then we place the points on the axes and from there we draw the line on the graph.
Complete step by step solution:
We are taking the general equation of line to understand the slope and the intercept form of the line
We change from the equation
The given equation is in the form of
We have to find the x-intercept, and y-intercept of the line
For this we convert the given equation into the form of
The given equation is
we get
We don’t find any intercepts as the form is not possible to create. This means the line intersects the axes at the same point. We can see that the line goes through the origin of

Note: A line parallel to the X-axis does not intersect the X-axis at any finite distance. Hence, we cannot get any finite x-intercept of such a line. Same goes for lines parallel to the Y-axis. In case of slope of a line the range of the slope is 0 to
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




