Question

How do you graph $y = 5x - 1$ ?

Answer 1

Hint: To plot a graph of any line, we need the points on the Cartesian coordinate plane. The points can be obtained by assuming different values for anyone coordinate and calculating the value for the other coordinate from the equation of a line.

Complete step-by-step answer:
Before plotting the line, first, we get some basic knowledge about the line with the Slope-Intercept equation of the line
$\Rightarrow$$y = mx + c$
Comparing the slope-intercept equation with the given line, we get
$\Rightarrow$$m = 5$ and $c = - 1$ .
The intercept on the Y axes is not $\;0$ , which shows that the line does not pass through the origin.
The slope of the line is greater than $\;1$ , which means the line is tilted more towards the Y-axes.
To plot the line, we start by plotting the X-intercept and Y-intercept
For the X-intercept, we consider y coordinate $y = 0$
Substituting this in the equation of the line
$ \Rightarrow 0 = 5x - 1$
Making $x$ the subject of the equation
$ \Rightarrow 5x = 1$
$ \Rightarrow x = \dfrac{1}{5}$
Hence the X-intercept of the line is $\left( {\dfrac{1}{5},0} \right)$ .
Now, for the Y-intercept, we consider x coordinate $x = 0$
Substituting this in the equation of the line
$ \Rightarrow y = 5(0) - 1$
$ \Rightarrow y = 0 - 1 = - 1$
Hence the Y-intercept of the line is $\left( {0, - 1} \right)$ .
We have two points of the line as $\left( {\dfrac{1}{5},0} \right)$ and $\left( {0, - 1} \right)$ .
Now, we can find some other points on the line.
Let’s suppose some values for the X coordinate and find the corresponding values of the Y coordinate from the equation.
Let’s assume $x = - 2$ and put this value in the equation of the line
$ \Rightarrow y = 5( - 2) - 1$
$ \Rightarrow y = - 10 - 1 = - 11$
Hence, we get the point with coordinates $( - 2, - 11)$
Now, let’s assume $x = 2$ and put this value in the equation of the line
$ \Rightarrow y = 5(2) - 1$
$ \Rightarrow y = 10 - 1 = 9$
Hence, we get the point with coordinates $(2,9)$
Plotting the four points we obtained $\left( {\dfrac{1}{5},0} \right)$ , $\left( {0, - 1} \right)$ , $( - 2, - 11)$, and $(2,9)$ we can plot the line on the graph as shown below.

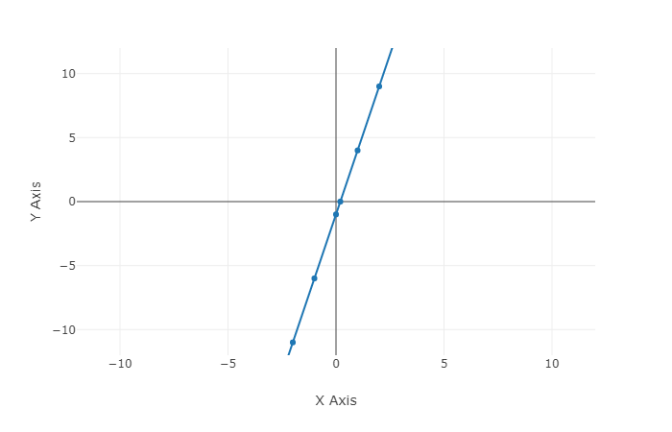
Note:
To plot a line, only two points are required. But we plot extra points to get a precise line and also to check if any mistake occurred while calculating or plotting the points that don’t fall on the line. Here we assumed the value of the X coordinate and calculated the value of the Y coordinate. The points can also be found by assuming the Y coordinate and calculating the X coordinate respectively.