
How do you graph
Answer
438.9k+ views
Hint: Since this graph is quite complex in the sense that we do not know any of its property, we will try to plot a few points of it find its periodicity and then with help of a graphing calculator see what the graph actually looks like. The first task ahead of us would be to find the periodicity of the given graph, since both of the term of the expression
Will have different periods, the lcm of the period of both the graphs will be the period of the compound oscillation of this graph , we will keep that in mind . The period of the
Complete step by step solution:
The given function,
Is a complex function, we have to first find periodicity . The period of the
Also we put few values and get the corresponding value the function gives,
Lets put
We get
We will put these values to plot a graph we will now see the graph from a calculator,
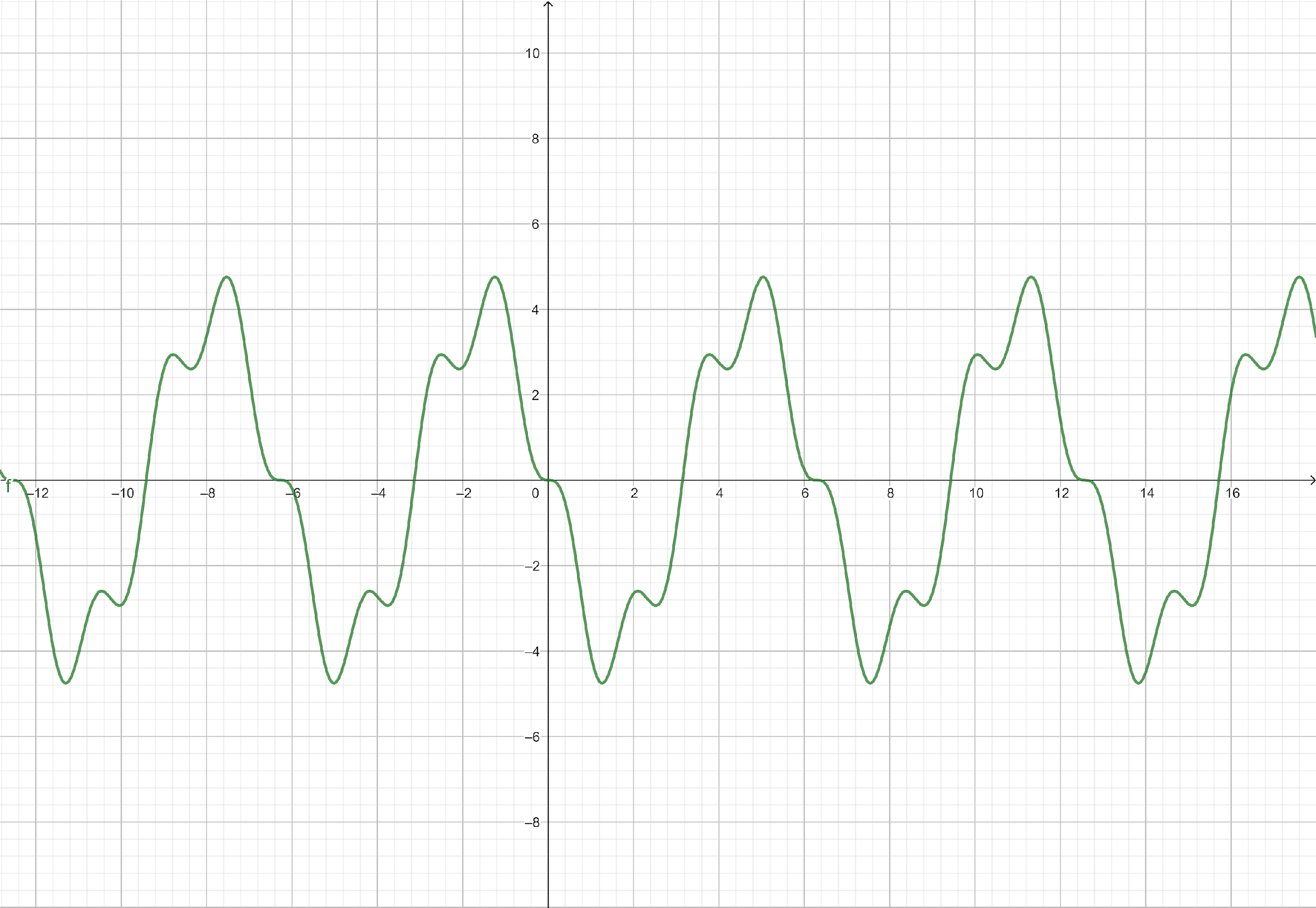
Note:
If a complex function is given then the period will be the LCM of periodicity all the terms in that given function.
Will have different periods, the lcm of the period of both the graphs will be the period of the compound oscillation of this graph , we will keep that in mind . The period of the
Complete step by step solution:
The given function,
Is a complex function, we have to first find periodicity . The period of the
Also we put few values and get the corresponding value the function gives,
Lets put
We get
We will put these values to plot a graph we will now see the graph from a calculator,

Note:
If a complex function is given then the period will be the LCM of periodicity all the terms in that given function.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




