Question

How do you graph $y = \sqrt {x + 4} $ ?

Answer 1

Hint:In order to determine the graph of the above equation, square on both sides of the equation, you will get an equation quadratic in variable $y$. So the graph will be a rightward opening parabola defined only for positive y-axis .Having the domain of the equation as $x \in \left[ { - 4,\infty } \right)$. Find out some good values of the equation by putting $x = - 3,0,5$ plot on the cartesian to get the accurate graph .

Complete step by step solution:
We are given a equation that is having two variables i.e.
$y = \sqrt {x + 4} $---(1)
Let’s find out the domain of the above equation, to know on what values of variable $x$the graph is going to be drawn.
We can clearly see that the $x + 4$ cannot be negative. Therefore, equation is defined for all $x + 4
\geqslant 0 \Rightarrow x \geqslant - 4$
$\therefore x \in \left[ { - 4,\infty } \right)$
We cannot directly sketch the graph of the above equation. So we will be square on both sides of the equation. We get,
$
{\left( y \right)^2} = {\left( {\sqrt {x + 4} } \right)^2} \\
{y^2} = x + 4\,\,\, - - - - - (2) \\
$
Graph will be a rightward opening parabola as the equation is quadratic in $y$
Since, from the equation (2) we can clearly see that the value of y is always positive.
So the graph is not defined for the negative y-axis.
Now we are going to graph, For that we are jumping on the cartesian plane.
Let's find out some good values of $x\, and \,y$, in other words some coordinates of points for equation (1).

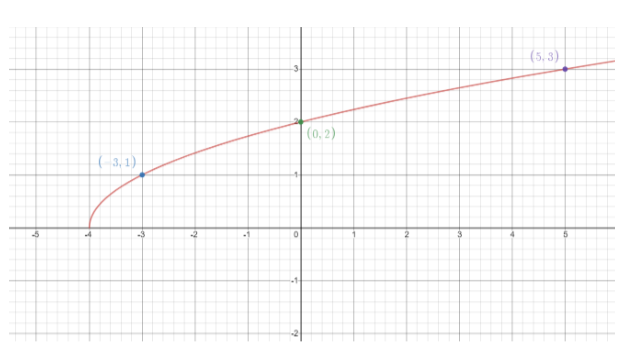
Hence we’ve successfully plotted our graph of $y = \sqrt {x + 4} $

Additional Information:
1.DOMAIN: Let R be a relation from a set A to a set B. Then the set of all first components or
coordinates of the ordered pairs belonging to R is called the domain of R.
Thus, domain of $R = \left\{ {a:(a,b) \in R} \right\}$
2.RANGE: Let R be a relation from a set A to a set B . Then the set of all second components or coordinates of the ordered pairs belonging to R is called the range of R.
Thus, Range of $R = \left\{ {b:\left( {a,b} \right) \in R} \right\}$

Note:
1. Cartesian Plane: A Cartesian Plane is given its name by the French mathematician Rene Descartes ,who first used this plane in the field of mathematics .It is defined as the two mutually perpendicular number line , the one which is horizontal is given name x-axis and the one which is vertical is known as y-axis. With the help of these axes we can plot any point on this cartesian plane with the help of an ordered pair of numbers.
2.Draw the cartesian plane only with the help of a straight ruler and pencil to get the perfect and accurate results.