
How do you graph
Answer
468.3k+ views
Hint:
To graph the function given, we need to locate the roots. We will use the fact that the function
Complete step by step solution:
We know that the period of the given function
This means that the function
So we can draw the graph of the given function in any interval of length
For this we need to choose the interval in which we make the graph. Before choosing it, let us try to locate the roots of
So the roots are located at
Also, we try to locate the asymptotes. We know that the asymptotes for
So let us choose our interval to be
From the above information, we can draw the graph of
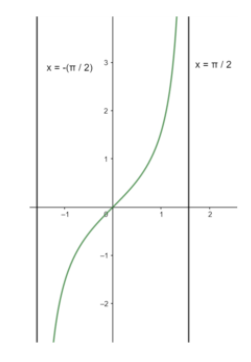
Since the function

Note:
Here, we might make a mistake by drawing the graph by plotting the points. This is because then we have to ensure proper scaling, and then we will not be able to obtain a rough sketch. Also, for obtaining the proper shape, we can consider the derivative of the function
To graph the function given, we need to locate the roots. We will use the fact that the function
Complete step by step solution:
We know that the period of the given function
This means that the function
So we can draw the graph of the given function in any interval of length
For this we need to choose the interval in which we make the graph. Before choosing it, let us try to locate the roots of
So the roots are located at
Also, we try to locate the asymptotes. We know that the asymptotes for
So let us choose our interval to be
From the above information, we can draw the graph of

Since the function

Note:
Here, we might make a mistake by drawing the graph by plotting the points. This is because then we have to ensure proper scaling, and then we will not be able to obtain a rough sketch. Also, for obtaining the proper shape, we can consider the derivative of the function
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

In which part of the body the blood is purified oxygenation class 11 biology CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




