Question

How do you graph \[y=2x-9\]?

Answer 1

Hint: Suppose an equation of straight line to be \[y=ax+b\]. We can draw the graph of \[y=ax+b\] from the simple graph \[y=x\]. We need to modify the \[y=x\] graph by shifting and scaling methods. It is a better idea to modify the graph of \[y=x\] in such a manner that we get the required graph by going from left side to right side of the equation \[y=2x-9\].

As per the given question, we need to graph a straight line which is given by the equation \[y=2x-9\].
A straight line can be traced out on the cartesian plane by just two points lying on it. We can also use a third point for sort of check. It is very simple to graph the \[y=x\] line as it is symmetric to both x and y axes.

The graph of \[y=x\] is as shown in below figure:

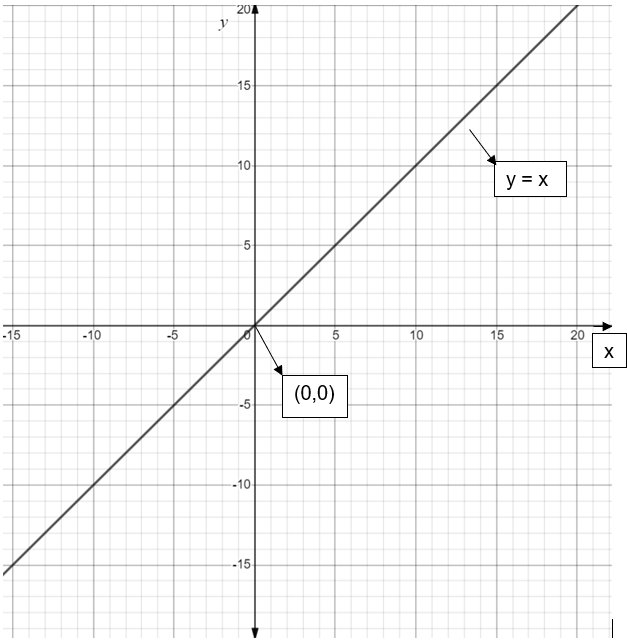
If we go from left hand side to right hand side of the equation \[y=2x-9\], it is clear that we need to first scale the \[y=x\] graph by a factor 2. Then we get, \[y=2x\].
And the graph of \[y=2x\] is as shown in the below figure:

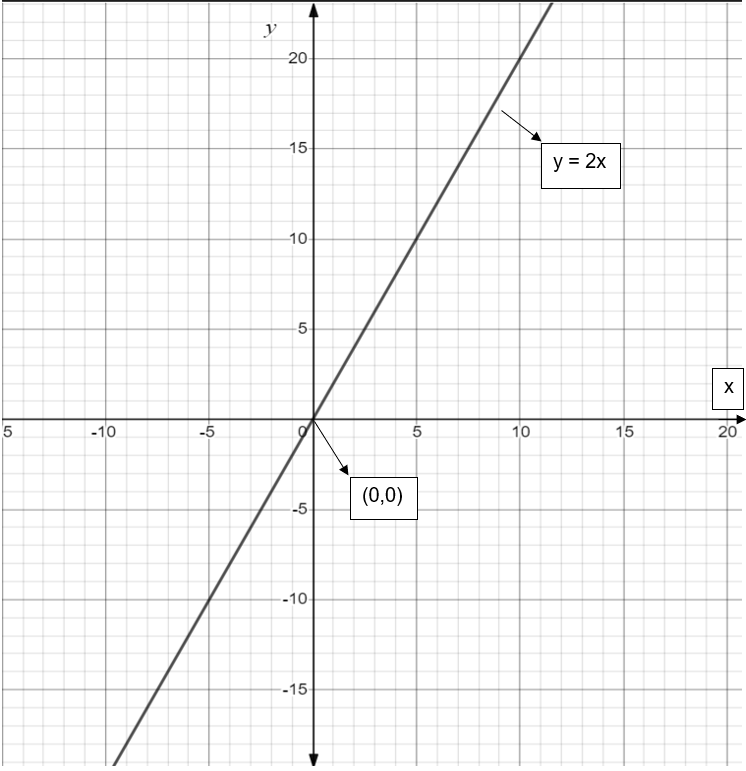
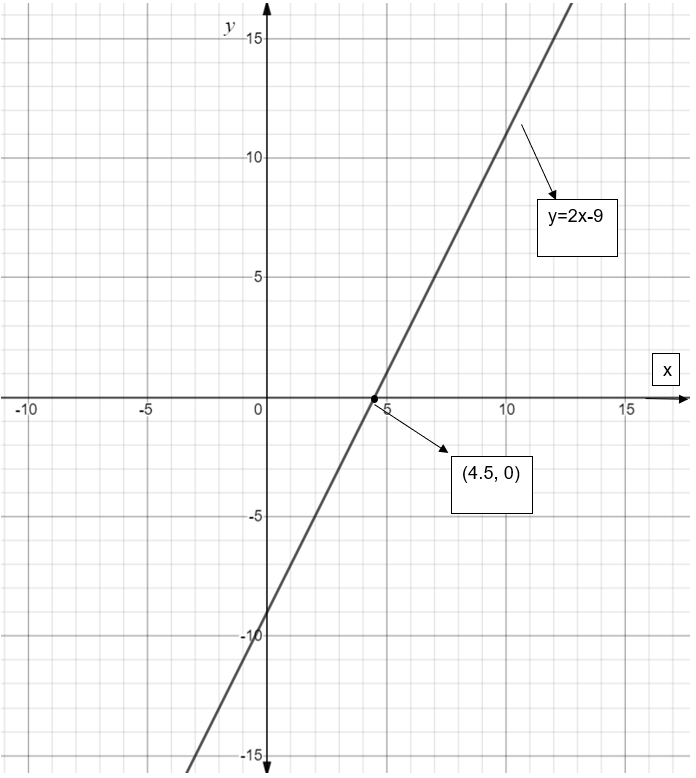
Now, we need to shift the \[y=2x\] graph right hand side by \[\dfrac{9}{2}\] units to get the required straight line \[y=2x-9\]. And the graph of \[y=2x-9\] is shown in the below figure:

\[\therefore \] We have to compress \[y=x\] by 2 and then shift it to the right hand side by \[\dfrac{9}{2}\] units to get the desired line \[y=2x-9\].

Note:
We can trace the graph of \[y=2x-9\] by substitution by any two random values of x. We can also trace the graph by going from the right hand side to left hand side of the straight-line equation \[y=2x-9\]. So, by taking 2 common, we get \[y=2(x-\dfrac{9}{2})\]. That is, we have to shift the \[y=x\] graph by \[\dfrac{9}{2}\] units and then compress it by a factor 2 to get the graph of \[y=2x-9\].