
How do you simplify
Answer
465.3k+ views
Hint: We will consider the inner function as an angle. Then we will eliminate the function
Formula used:
Complete step by step solution:
We are required to simplify the expression
Let us begin by denoting the innermost function, which is
Let us try to eliminate the function
We will use the property
Let us consider a right triangle ABC with right-angle
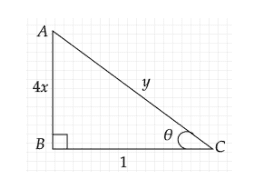
Now, from equation
We know that in a right-triangle ABC,
Now, we have to find the hypotenuse of the right triangle with sides
By Pythagoras theorem, we have
Taking square root on both sides of the above expression, we get
We are supposed to find the value of
We know that
Note:
The functions
Formula used:
Complete step by step solution:
We are required to simplify the expression
Let us begin by denoting the innermost function, which is
Let us try to eliminate the function
We will use the property
Let us consider a right triangle ABC with right-angle

Now, from equation
We know that in a right-triangle ABC,
Now, we have to find the hypotenuse of the right triangle with sides
By Pythagoras theorem, we have
Taking square root on both sides of the above expression, we get
We are supposed to find the value of
We know that
Note:
The functions
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




