Question

How do you solve and graph \[8x > 7x-4\]?

Answer 1

Hint: Any inequality can be solved by taking all the constants to one side and all the unknowns to the other side of the equation. The constant side must be solved step-by-step to get through the solution. We can use the distributive property and do the addition, subtraction, multiplication and division operations wherever necessary in such a way to simplify the inequality.
As per the given question, we are provided with an inequality which is to be simplified to plot a graph. Here, the given inequality is \[8x > 7x-4\].

Complete step by step answer:
In the given equation, we have to isolate x by adding \[-7x\] to both sides of the equation. Here, addition of \[-7x\] and \[7x\] is nothing which is equal to zero. And, addition of \[8x\] with \[-7x\] is equal to \[x\]. Then, on substituting these values, we get
\[\begin{align}
  & \Rightarrow 8x > 7x-4 \\
 & \Rightarrow 8x-7x > 7x-7x-4 \\
 & \Rightarrow x > 0-4 \\
 & \Rightarrow x > -4 \\
\end{align}\]
On solving the inequality we got the inequality as \[x > -4\]. This inequality implies that we need to draw a graph \[x=-4\]. \[x=-4\] is a vertical line meeting x-axis at \[(-4,0)\]. The line will be a dashed line because the inequality operator does not contain an “or equal to” clause. Therefore, we shade to the right side of the line because the inequality operator contains a “greater than” clause.

The graph of \[x > -4\] is as shown in below figure:

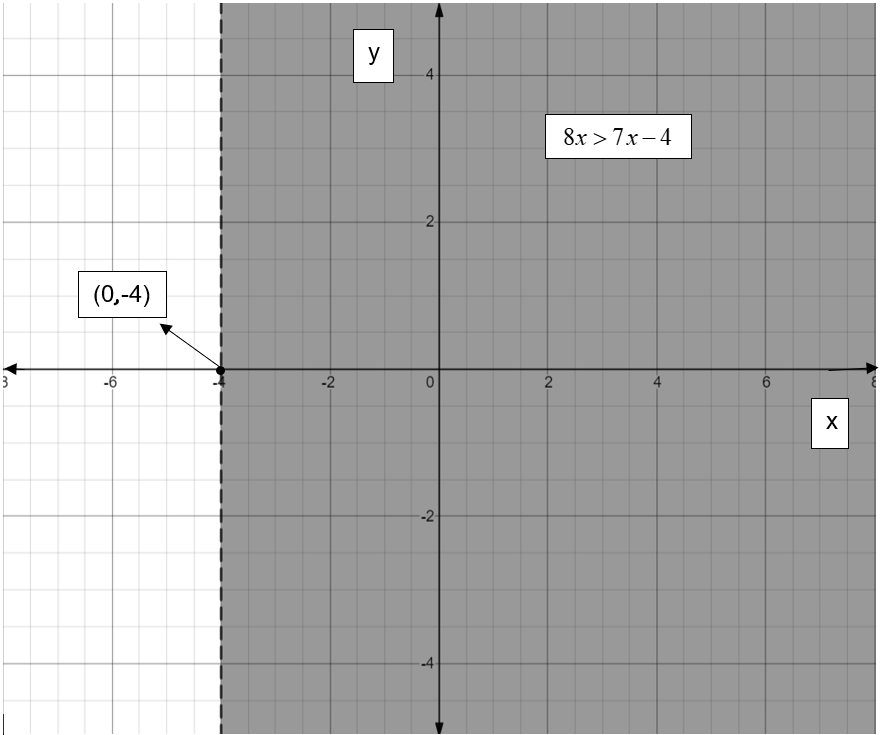
Therefore, we have to draw a vertical line at \[(-4,0)\]and shade the part right side to the line to get the desired plot \[8x > 7x-4\].

Note:
While solving inequalities check which inequality is given carefully to avoid mistakes. We have to check which part to be shaded depending on the inequality given in the problem. We should avoid calculation mistakes to get the correct solution.