Question

How do you solve $ \sin 3x=0 $ ?

Answer 1

Hint: We first find the principal value of x for which $ \sin 3x=0 $ . In that domain, equal value of the same ratio gives equal angles. We find the angle value for x. at the end we also find the general solution for the equation $ \sin 3x=0 $ .

Complete step-by-step answer:
It’s given that $ \sin 3x=0 $ . The value in question is 0. We need to find x for which $ \sin 3x=0 $ .
We know that in the principal domain or the periodic value of
$ -\dfrac{\pi }{2}\le x\le \dfrac{\pi }{2} $ for $ \sin x $ , if we get $ \sin a=\sin b $ where
$ -\dfrac{\pi }{2}\le a,b\le \dfrac{\pi }{2} $ then $ a=b $ . We have the value of
$ \sin \left( 0 \right) $ as 0. $ -\dfrac{\pi }{2}<0<\dfrac{\pi }{2} $ .
Therefore,
$ \sin \left( 3x \right)=0=\sin \left( 0 \right) $ which gives $ 3x=0 $ .
For ,
$ \sin 3x=0 $ , the value of $ 3x $ is $ 3x=0 $ . Solving the equation, we get $ x=0 $ .
We also can show the solutions (primary and general) of the equation $ \sin 3x=0 $ through the graph. We take $ y=\sin 3x=0 $ . We got two equations $ y=\sin \left( 3x \right) $ and
$ y=0 $ . We place them on the graph and find the solutions as their intersecting points.
We can see the primary solution in the interval $ -\dfrac{\pi }{2}\le x\le \dfrac{\pi }{2} $ is the point A as $ x=0 $ .
All the other intersecting points of the curve and the line are general solutions.

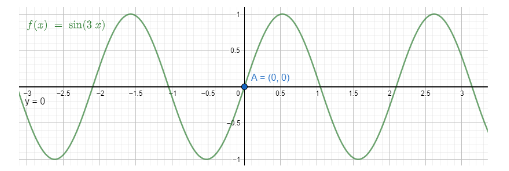
We can see the primary solution in the interval $-\dfrac{\pi }{2}\le x\le \dfrac{\pi }{2}$ is the point A as $x=0$.
So, the correct answer is “ $x=0$ OR $ x=\dfrac{n\pi }{3} $”.

Note: Although for elementary knowledge the principal domain is enough to solve the problem. But if mentioned to find the general solution then the domain changes to $ -\infty \le x\le \infty $ . In that case we have to use the formula $ x=n\pi +{{\left( -1 \right)}^{n}}a $ for $ \sin \left( x \right)=\sin a $ where $ -\dfrac{\pi }{2}\le a\le \dfrac{\pi }{2} $ . For our given problem $ \sin 3x=0 $ , the general solution will be $ 3x=n\pi +{{\left( -1 \right)}^{n}}\times 0=n\pi $ . Here $ n\in \mathbb{Z} $ .
The simplified general solution for the equation $ \sin 3x=0 $ will be $ x=\dfrac{n\pi }{3} $ .