Question

How do you solve \[x - 5 < 8\]?

Answer 1

Hint: Here we have to find the value of \[x\] by solving the given inequality i.e., \[x - 5 < 8\]. These types of problems are solved using various mathematical operations such as addition, subtraction, multiplication and division. A linear inequality is inequality in which one has the highest degree of one. We will use basic mathematical operations in addition to simplify this linear inequality.

Complete step by step solution:
Given that \[x - 5 < 8\]. As we know , inequality remains the same if we add a positive constant on both sides of an inequality.
Adding \[5\] on both the sides, we get
\[ \Rightarrow x - 5 + 5 < 8 + 5\]
On simplification, we get
\[ \Rightarrow x < 13\]
Therefore, the value of \[x\] is less than \[13\].
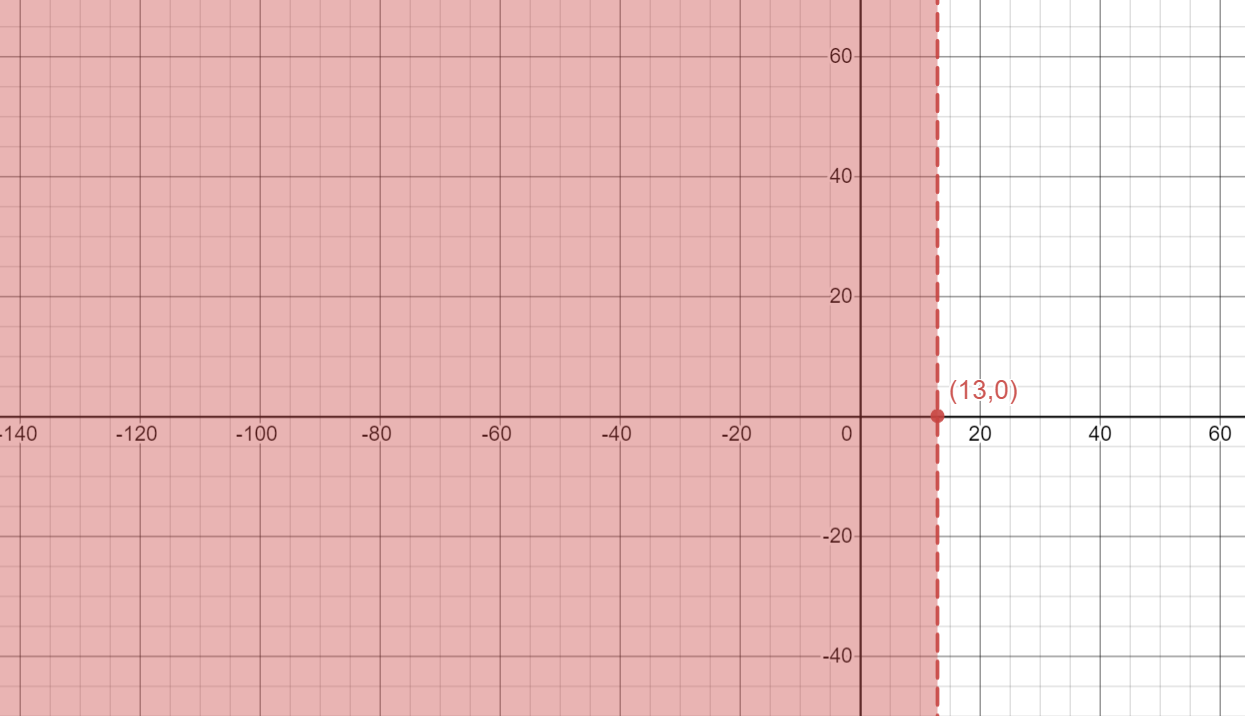
This solution of $x$ can be seen in the following graph: (Red color represents the solution of $x$).

Additional information:
In these types of questions, the most important is to know basic mathematical operations.
Addition is the operation in which two numbers are combined to get the result.
Subtraction is the operation that gives us the difference between the two numbers.
Multiplication is the operation in which one number is added to itself for some particular number of times.
Division is the operation in which the dividend is divided by the divisor to get the quotient along with some remainder.

Note:
Here we are required to know that while solving complex types of equations, we have to use the rule of BODMAS. BODMAS is defined as B: Bracket, O: Of, D: Division and M: Multiplication. We should apply the mathematical operations in a particular order which is given by the letters of BODMAS.