Question

How do you solve \[{{x}^{2}}+2x-3=0\] graphically?

Answer 1

Hint: To solve this graphically, we have to find out if it touches the x-axis using discriminant given by \[\Delta ={{b}^{2}}-4ac\] for function \[y=a{{x}^{2}}+bx+c\] . Then, we will find the local maxima or minima by differentiating the function equating to 0 and hence obtaining the value of x. Similarly, finding the second derivative and equating to 0 will give us the value of y. Again, we will substitute x as 0 and 1 in the function and obtain another set of points. We will then be able to plot the graph and find values of x.

Complete step-by-step solution:
From the question, we were given to draw the graph of the quadratic equation \[{{x}^{2}}+2x-3=0\].
Let us consider the values of x are on the x-axis and the obtained values of y on y-axis.
Now let us find the discriminant of the quadratic equation \[{{x}^{2}}+2x-3=0\].
We know that if the discriminant of quadratic equation \[y=a{{x}^{2}}+bx+c\] is equal to \[\Delta \], then \[\Delta ={{b}^{2}}-4ac\].
So, let us assume the discriminant of the quadratic equation \[{{x}^{2}}+2x-3=0\] is equal to \[\Delta \]. Then \[\Rightarrow \Delta =4-4\left( 1 \right)\left( -3 \right)=16> 0\].
So, it is clear that the discriminant of the quadratic equation is greater than zero.
We know that if the discriminant of the quadratic equation \[y=a{{x}^{2}}+bx+c\] is greater than zero, then the quadratic equation will have real roots. So, we can say that if the discriminant of the quadratic equation \[y=a{{x}^{2}}+bx+c\] is greater than zero, then the graph will touch the x-axis.
So, it is clear that the graph of the quadratic equation \[{{x}^{2}}+2x-3=0\] touches the x-axis.
Now let us find whether the quadratic equation \[{{x}^{2}}+2x-3=0\] has local maxima or local minima.
We know that a function f(x) has local maxima or local minima at the point where the derivative of f(x) is equal to zero. So, let us find the points whether the quadratic equation \[{{x}^{2}}+2x-3=0\] has a local maximum or local minimum.
Let us assume the derivative of function \[{{x}^{2}}+2x-3=y\] is equal to \[{y}'\].
\[\Rightarrow {y}'=\dfrac{dy}{dx}=\dfrac{d}{dx}\left( {{x}^{2}}+2x-3 \right)=2x+2\]
Now we should find the value of x where \[{y}'\] is equal to zero.
\[\Rightarrow 2x+2=0\]
\[\Rightarrow 2x=-2\]
\[\Rightarrow x=-1\]
So, it is clear that at \[\Rightarrow x=-1\] we will have a local maxima or local minima for \[{{x}^{2}}+2x-3=y\].
Now we should check whether \[\Rightarrow x=-1\] is a local maxima or local minima.
We know that the value of x where \[{f}''(x)> 0\] and \[{f}'(x)=0\] is said to be point of minima and the value of x where \[{f}''(x)<0\] and \[{f}'(x)=0\] is said to be point of maxima.
So, let us assume the second derivative of \[{{x}^{2}}+2x-3=y\] is equal to \[{y}''\].
\[\Rightarrow {y}''=\dfrac{d{y}'}{dx}=\dfrac{d}{dx}\left( 2x+2 \right)=2>0\]
So, it is clear that the second derivative of \[{{x}^{2}}+2x-3=y\] is greater than zero. So, we can say that \[\Rightarrow x=-1\] is the point of local minima.
Now let us find the value of y where \[\Rightarrow x=-1\]
\[\Rightarrow y={{\left( -1 \right)}^{2}}+2(-1)-3\]
\[\Rightarrow y=-4\]
So, we can say that the minimum value of \[{{x}^{2}}+2x-3=y\] is at \[\Rightarrow x=-1\]
So, it is clear that \[\left( -1,-4 \right)\] lies on the graph \[{{x}^{2}}+2x-3=y\].
So, it is clear that the graph of \[y={{x}^{2}}+4x+6\] is in the second quadrant and mostly first quadrant.
Now let us substitute the value of x is equal to zero in \[{{x}^{2}}+2x-3=y\].
Then we get
\[\Rightarrow y=0+0-3=-3\]
So, we can say that \[\left( 0,-3 \right)\] lies on the graph \[{{x}^{2}}+2x-3=y\].
Now let us substitute the value of x is equal to 1.
Then we get
\[\Rightarrow 1+2-3=y\]
\[\Rightarrow y=0\]
So, we can say that \[\left( 1,0 \right)\] lies on the graph \[{{x}^{2}}+2x-3=y\].
Now let us draw a parabola passing through the points which we found as shown below.

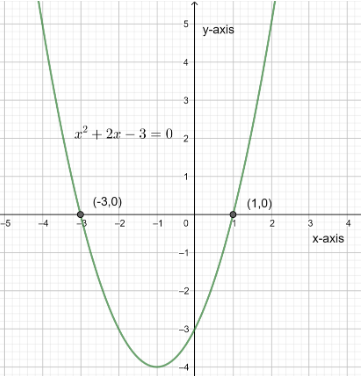
Note: We must be very careful while doing the problems of the graphical ones and one must be knowing the basic concept of finding points on the graph so that they can draw the required graph and must be aware of the concept of differentiation and must be knowing the theory about differentiation. We can also find points or check weather the point lies on the graph or not by substitution method example we substitute x=1 in equation \[\Rightarrow y={{x}^{2}}+2x-3\] \[\Rightarrow y=3-3\] \[\Rightarrow y=0\] so the point \[\left( 1,0 \right)\] lies on the graph.