Question

(i) A book is kept on the table as shown in the diagram. Copy the diagram and mark the action and reaction forces with their directions.

(ii) Do these forces act on the same body or two different bodies?
(iii) State Newton’s second law of motion.
(iv) Find the force exerted on a mass of \[20{\text{g}}\] if the acceleration produced in it is $8{\text{ m}}{{\text{s}}^{ - 2}}$.
(v) The change in momentum of a body is represented by $\Delta p = m \times \Delta v$. When is the expression valid for the change in the linear momentum?

Answer 1

Hint: All the questions are based on Newton’s law of motion. In the first case, the book is at rest so only resting forces will be applicable. When a body accelerates it exerts a force that is equal to its product of mass and acceleration.

Complete step by step answer:
(i) We will draw the diagram and label the forces in it.

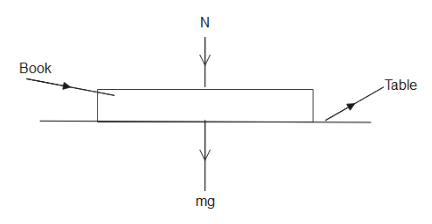
As the book is at rest therefore it will experience only the force due to its weight and the normal force.

(ii) For the second we are asked if the force acts on the same body. The forces act on the same body.

(iii) We need to state Newton’s law of motion. Newton’s second law of motion states that the range of change of momentum of a body is directly proportional to the force applied on it, and the momentum occurs in the direction of the net applied force. For the body of mass $m$, Newton’s law formula is given as
$F = ma$
Where $m$ is the mass of the object, $F$ is applied force and $a$ is the acceleration produced.

(iv) We are given the mass and the acceleration produced and we need to find the force which can be calculated using the above formula. Hence substituting the value we get
$ \Rightarrow F = 20 \times 8 = 160{\text{N}}$

(v) We need to find the validity of the given expression.The change in momentum of a body is given by $\Delta p = m \times \Delta v$, thus momentum of a given mass is $P = mv$.Assuming the system mass remains constant and the system is accelerating, thus
${P_i} = m{v_i}$ and ${P_f} = m{v_f}$
Therefore the change in momentum will be
\[\Delta p = {P_f} - {P_i}\]
Substituting the formula for momentum
$ \Rightarrow \Delta p = m({v_f} - {v_{_i}})$
$ \therefore \Delta p = m \times \Delta v$
The expression is valid for a change in linear momentum when there is a change in linear velocity.

Note: Momentum is a vector quantity having both velocity and direction. When force is applied to a body, it can either change its momentum or its velocity, or both. If the net force acting on the body is positive, the body gets accelerated.