Question

I is the incenter of triangle ABC, AD is the angle bisector of A then AI: ID=
(A) $a+b:c$
(B) $b+c:a$
 (C) $c+a:b$
(D) $b:c$

Answer 1

Hint: The center of incircle of a triangle is the incenter of the triangle. The line joining any point of the triangle to the incenter is the angle bisector of that angle. So we can tell the intersection of all 3 angle bisectors is incenter. If AD is the angle bisector of A then incenter then incenter I lies on AD.

Complete step by step answer:
I is the incenter of triangle ABC and AD is the angle bisector of A. Drawing the figure-

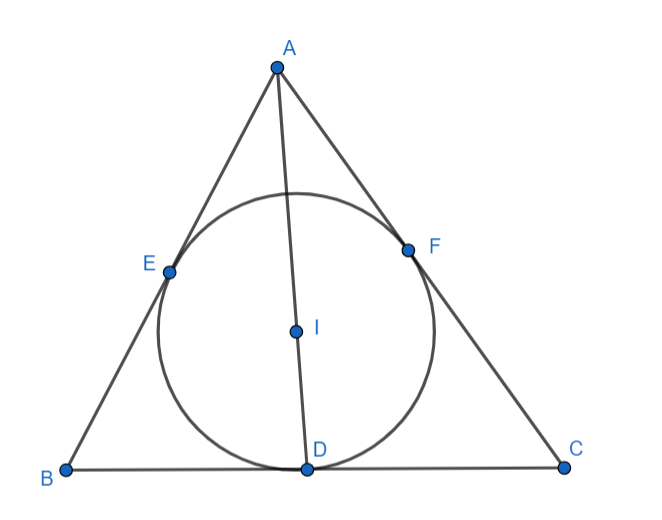
In the above figure point E is the touching point of Line AB with the incircle and point F is the touching point of line AC with circle.
So radius of the incircle IE=IF
Angle BAD =Angle DAC= $\dfrac{A}{2}$
Let’s find out the length of the angle bisector AD. We can find the length by area method.
We know that area of any triangle= $\dfrac{1}{2}$$\times $ product of any 2 consecutive sides $\times $ sin of angle between them
So we can write area of triangle ABC= $\dfrac{1}{2}\times AB\times AC\times \sin A$ ….eq1
Another way of writing area of triangle ABC= Area of triangle ABD+ area of triangle ADC
= $\left( \dfrac{1}{2}\times AB\times AD\times \sin \dfrac{A}{2} \right)+\left( \dfrac{1}{2}\times AD\times AC\times \sin \dfrac{A}{2} \right)$
Taking $\dfrac{1}{2}\times AD\times \sin \dfrac{A}{2}$ common
Area of triangle ABC= $\dfrac{1}{2}\times AD\times \sin \dfrac{A}{2}\left( AB+AC \right)$ ….eq2
Comparing eq1 and eq2
$\dfrac{1}{2}\times AD\times \sin \dfrac{A}{2}\left( AB+AC \right)=\dfrac{1}{2}\times AB\times AC\times \sin A$
So, $AD=\dfrac{AB\times AC\times \sin A}{\left( AB+AC \right)\sin \dfrac{A}{2}}$
$\Rightarrow AD=\dfrac{2\times AB\times AC\times \cos \dfrac{A}{2}}{AB+AC}$ …….eq3
Let’s find out the length of AI. Triangle AEI is a right angled triangle and angle EAI is $\dfrac{A}{2}$ .So the length of AI= $\dfrac{IE}{\sin \dfrac{A}{2}}$ and IE is the radius of incircle
Formula for radius of incircle = Area of triangle divided by s where $s=\dfrac{AB+BC+CA}{2}$
So $IE=\dfrac{\dfrac{1}{2}\times AB\times AC\times \sin A}{\dfrac{1}{2}\times \left( AB+BC+CA \right)}$
$AI=\dfrac{IE}{\sin \dfrac{A}{2}}$
$\Rightarrow \dfrac{IE}{\sin \dfrac{A}{2}}=\dfrac{2\times AB\times AC\times \cos \dfrac{A}{2}}{AB+BC+CA}$
$\Rightarrow AI=\dfrac{2\times AB\times AC\times \cos \dfrac{A}{2}}{AB+BC+CA}$…..eq4
In eq3 and eq4 we have length of AD and AI
$\dfrac{AI}{AD}=\dfrac{AB+AC}{AB+BC+AC}$
If we name AB as c , BC as a and AC as b
$\dfrac{AI}{AD}=\dfrac{b+c}{a+b+c}$ ….eq5
$AD=AI+ID$
Dividing by AD we get
$\dfrac{ID}{AD}=1-\dfrac{AI}{AD}$
$\dfrac{ID}{AD}=\dfrac{a}{a+b+c}$ …..eq6

Dividing eq5 by eq6
$\dfrac{AD}{ID}=\dfrac{b+c}{a}$
So ratio between $AD:ID=b+c:a$

So, the correct answer is “Option B”.

Note: Don’t get confused between circumcenter and incenter. Circumcenter is the center of circumcircle which is outside the triangle and incenter is the center of the incircle which is inside the triangle. Intersection of perpendicular bisectors of sides is circumcenter and intersection of angle bisectors of all angles is incenter. To solve these types of questions it is good to remember the formula for length of angle bisector and radius of incircle.