
How do identify the important parts of $y = - 7{x^2}$ to graph it?
Answer
436.5k+ views
Hint: We have to find the properties of the given parabola. First rewrite the equation in vertex form. Next, use the vertex form of parabola, to determine the values of $a$, $h$, and $k$. Next, find the vertex and the distance from the vertex to the focus. Then, find the focus, axis of symmetry and directrix. Use the properties of the parabola to analyse and graph the parabola. Select a few $x$ values, and plug them into the equation to find the corresponding $y$ values. The $x$ values should be selected around the vertex. Graph the parabola using its properties and the selected points.
Formula used:
Vertex form of a parabola: $a{\left( {x + d} \right)^2} + e$
$d = \dfrac{b}{{2a}}$
$e = c - \dfrac{{{b^2}}}{{4a}}$
Vertex form: $y = a{\left( {x - h} \right)^2} + k$
Vertex: $\left( {h,k} \right)$
$p = \dfrac{1}{{4a}}$
Focus: $\left( {h,k + p} \right)$
Directrix: $y = k - p$
Complete step by step answer:
We have to find the properties of the given parabola.
So, first rewrite the equation in vertex form.
For this, complete the square for $ - 7{x^2}$.
Use the form $a{x^2} + bx + c$, to find the values of $a$, $b$, and $c$.
$a = - 7,b = 0,c = 0$
Consider the vertex form of a parabola.
$a{\left( {x + d} \right)^2} + e$
Now, substitute the values of $a$ and $b$ into the formula $d = \dfrac{b}{{2a}}$.
$d = \dfrac{0}{{2\left( { - 7} \right)}}$
Simplify the right side.
$ \Rightarrow d = 0$
Find the value of $e$ using the formula $e = c - \dfrac{{{b^2}}}{{4a}}$.
$e = 0 - \dfrac{{{0^2}}}{{4\left( { - 7} \right)}}$
$ \Rightarrow e = 0$
Now, substitute the values of $a$, $d$, and $e$ into the vertex form $a{\left( {x + d} \right)^2} + e$.
$ - 7{x^2}$
Set $y$ equal to the new right side.
$y = - 7{x^2}$
Now, use the vertex form, $y = a{\left( {x - h} \right)^2} + k$, to determine the values of $a$, $h$, and $k$.
$a = - 7$
$h = 0$
$k = 0$
Since the value of $a$ is negative, the parabola opens down.
Opens Down
Find the vertex $\left( {h,k} \right)$.
$\left( {0,0} \right)$
Now, find $p$, the distance from the vertex to the focus.
Find the distance from the vertex to a focus of the parabola by using the following formula.
$\dfrac{1}{{4a}}$
Substitute the value of $a$ into the formula.
$\dfrac{1}{{4\left( { - 7} \right)}}$
Multiply $4$ by $ - 7$, we get
$ \Rightarrow - \dfrac{1}{{28}}$
Find the focus.
The focus of a parabola can be found by adding $p$ to the $y$-coordinate $k$ if the parabola opens up or down.
$\left( {h,k + p} \right)$
Now, substitute the known values of $h$, $p$, and $k$ into the formula and simplify.
$\left( {0, - \dfrac{1}{{28}}} \right)$
Find the axis of symmetry by finding the line that passes through the vertex and the focus.
$x = 0$
Find the directrix.
The directrix of a parabola is the horizontal line found by subtracting $p$ from the $y$-coordinate $k$ of the vertex if the parabola opens up or down.
$y = k - p$
Now, substitute the known values of $p$ and $k$ into the formula and simplify.
$y = \dfrac{1}{{28}}$
Use the properties of the parabola to analyse and graph the parabola.
Direction: Opens Down
Vertex: $\left( {0,0} \right)$
Focus: $\left( {0, - \dfrac{1}{{28}}} \right)$
Axis of Symmetry: $x = 0$
Directrix: $y = \dfrac{1}{{28}}$
Select a few $x$ values, and plug them into the equation to find the corresponding $y$ values. The $x$ values should be selected around the vertex.
Replace the variable $x$ with $ - 1$ in the expression.
$f\left( { - 1} \right) = - 7{\left( { - 1} \right)^2}$
Simplify the result.
$f\left( { - 1} \right) = - 7$
The final answer is $ - 7$.
The $y$ value at $x = - 1$ is $ - 7$.
$y = - 7$
Replace the variable $x$ with $ - 2$ in the expression.
\[f\left( { - 2} \right) = - 7{\left( { - 2} \right)^2}\]
Simplify the result.
\[f\left( { - 2} \right) = - 28\]
The final answer is $ - 28$.
The $y$ value at $x = - 2$ is $ - 28$.
$y = - 28$
Replace the variable $x$ with $1$ in the expression.
$f\left( 1 \right) = - 7{\left( 1 \right)^2}$
Simplify the result.
$f\left( 1 \right) = - 7$
The final answer is $ - 7$.
The $y$ value at $x = 1$ is $ - 7$.
$y = - 7$
Replace the variable $x$ with $2$ in the expression.
\[f\left( 2 \right) = - 7{\left( 2 \right)^2}\]
Simplify the result.
\[f\left( 2 \right) = - 28\]
The final answer is $ - 28$.
The $y$ value at $x = 2$ is $ - 28$.
$y = - 28$
Graph the parabola using its properties and the selected points.
Direction: Opens Down
Vertex: $\left( {0,0} \right)$
Focus: $\left( {0, - \dfrac{1}{{28}}} \right)$
Axis of Symmetry: $x = 0$
Directrix: $y = \dfrac{1}{{28}}$
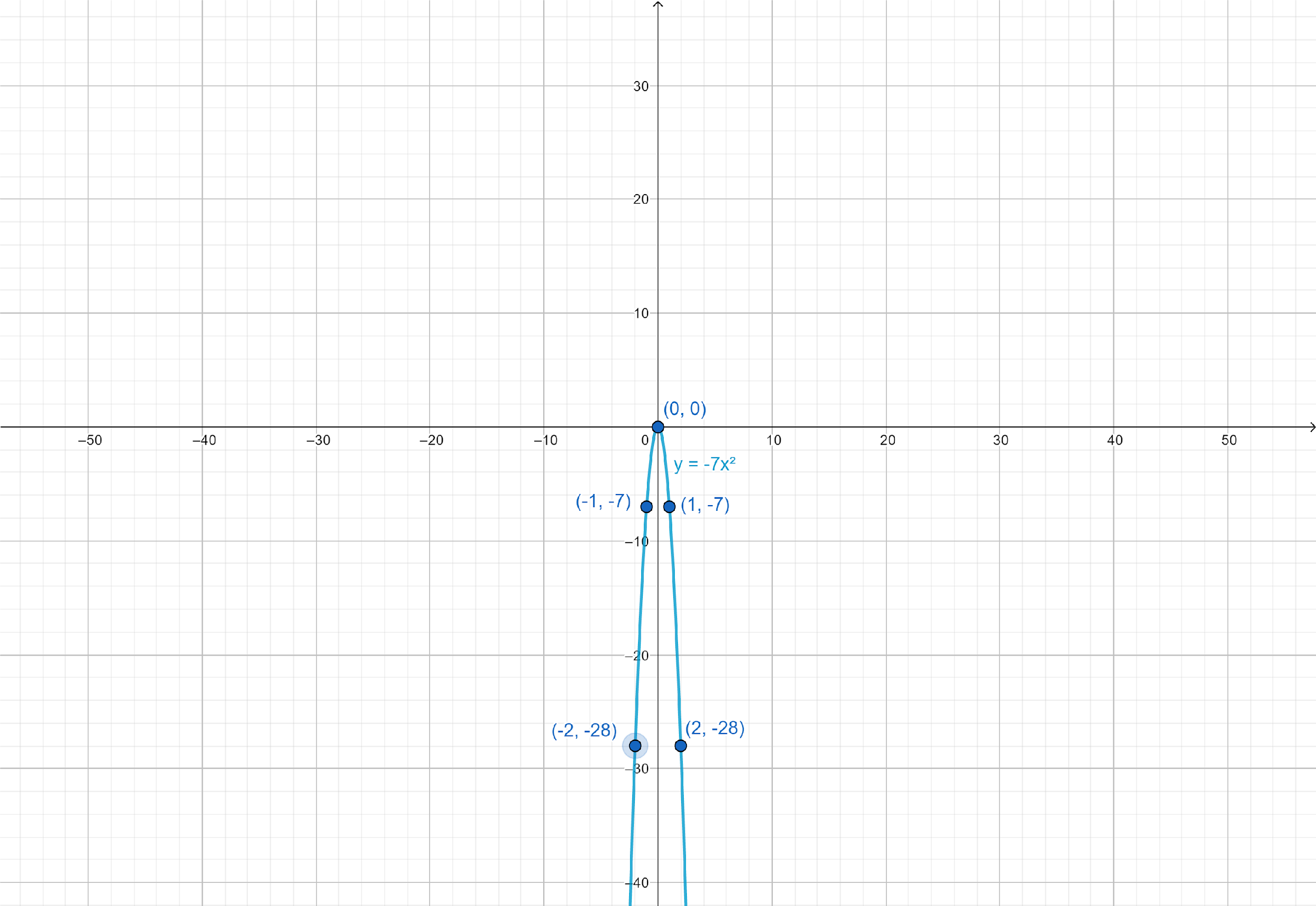
Note: Graph of $y = 7{x^2}$ will open upwards with vertex at centre, focus at $\left( {0,\dfrac{1}{{28}}} \right)$, axis of symmetry $x = 0$ and directrix $y = - \dfrac{1}{{28}}$. It means a mirror image of $y = - 7{x^2}$.
Formula used:
Vertex form of a parabola: $a{\left( {x + d} \right)^2} + e$
$d = \dfrac{b}{{2a}}$
$e = c - \dfrac{{{b^2}}}{{4a}}$
Vertex form: $y = a{\left( {x - h} \right)^2} + k$
Vertex: $\left( {h,k} \right)$
$p = \dfrac{1}{{4a}}$
Focus: $\left( {h,k + p} \right)$
Directrix: $y = k - p$
Complete step by step answer:
We have to find the properties of the given parabola.
So, first rewrite the equation in vertex form.
For this, complete the square for $ - 7{x^2}$.
Use the form $a{x^2} + bx + c$, to find the values of $a$, $b$, and $c$.
$a = - 7,b = 0,c = 0$
Consider the vertex form of a parabola.
$a{\left( {x + d} \right)^2} + e$
Now, substitute the values of $a$ and $b$ into the formula $d = \dfrac{b}{{2a}}$.
$d = \dfrac{0}{{2\left( { - 7} \right)}}$
Simplify the right side.
$ \Rightarrow d = 0$
Find the value of $e$ using the formula $e = c - \dfrac{{{b^2}}}{{4a}}$.
$e = 0 - \dfrac{{{0^2}}}{{4\left( { - 7} \right)}}$
$ \Rightarrow e = 0$
Now, substitute the values of $a$, $d$, and $e$ into the vertex form $a{\left( {x + d} \right)^2} + e$.
$ - 7{x^2}$
Set $y$ equal to the new right side.
$y = - 7{x^2}$
Now, use the vertex form, $y = a{\left( {x - h} \right)^2} + k$, to determine the values of $a$, $h$, and $k$.
$a = - 7$
$h = 0$
$k = 0$
Since the value of $a$ is negative, the parabola opens down.
Opens Down
Find the vertex $\left( {h,k} \right)$.
$\left( {0,0} \right)$
Now, find $p$, the distance from the vertex to the focus.
Find the distance from the vertex to a focus of the parabola by using the following formula.
$\dfrac{1}{{4a}}$
Substitute the value of $a$ into the formula.
$\dfrac{1}{{4\left( { - 7} \right)}}$
Multiply $4$ by $ - 7$, we get
$ \Rightarrow - \dfrac{1}{{28}}$
Find the focus.
The focus of a parabola can be found by adding $p$ to the $y$-coordinate $k$ if the parabola opens up or down.
$\left( {h,k + p} \right)$
Now, substitute the known values of $h$, $p$, and $k$ into the formula and simplify.
$\left( {0, - \dfrac{1}{{28}}} \right)$
Find the axis of symmetry by finding the line that passes through the vertex and the focus.
$x = 0$
Find the directrix.
The directrix of a parabola is the horizontal line found by subtracting $p$ from the $y$-coordinate $k$ of the vertex if the parabola opens up or down.
$y = k - p$
Now, substitute the known values of $p$ and $k$ into the formula and simplify.
$y = \dfrac{1}{{28}}$
Use the properties of the parabola to analyse and graph the parabola.
Direction: Opens Down
Vertex: $\left( {0,0} \right)$
Focus: $\left( {0, - \dfrac{1}{{28}}} \right)$
Axis of Symmetry: $x = 0$
Directrix: $y = \dfrac{1}{{28}}$
Select a few $x$ values, and plug them into the equation to find the corresponding $y$ values. The $x$ values should be selected around the vertex.
Replace the variable $x$ with $ - 1$ in the expression.
$f\left( { - 1} \right) = - 7{\left( { - 1} \right)^2}$
Simplify the result.
$f\left( { - 1} \right) = - 7$
The final answer is $ - 7$.
The $y$ value at $x = - 1$ is $ - 7$.
$y = - 7$
Replace the variable $x$ with $ - 2$ in the expression.
\[f\left( { - 2} \right) = - 7{\left( { - 2} \right)^2}\]
Simplify the result.
\[f\left( { - 2} \right) = - 28\]
The final answer is $ - 28$.
The $y$ value at $x = - 2$ is $ - 28$.
$y = - 28$
Replace the variable $x$ with $1$ in the expression.
$f\left( 1 \right) = - 7{\left( 1 \right)^2}$
Simplify the result.
$f\left( 1 \right) = - 7$
The final answer is $ - 7$.
The $y$ value at $x = 1$ is $ - 7$.
$y = - 7$
Replace the variable $x$ with $2$ in the expression.
\[f\left( 2 \right) = - 7{\left( 2 \right)^2}\]
Simplify the result.
\[f\left( 2 \right) = - 28\]
The final answer is $ - 28$.
The $y$ value at $x = 2$ is $ - 28$.
$y = - 28$
| $x$ | $y$ |
| $ - 2$ | $ - 28$ |
| $ - 1$ | $ - 7$ |
| $0$ | $0$ |
| $1$ | $ - 7$ |
| $2$ | $ - 28$ |
Graph the parabola using its properties and the selected points.
Direction: Opens Down
Vertex: $\left( {0,0} \right)$
Focus: $\left( {0, - \dfrac{1}{{28}}} \right)$
Axis of Symmetry: $x = 0$
Directrix: $y = \dfrac{1}{{28}}$
| $x$ | $y$ |
| $ - 2$ | $ - 28$ |
| $ - 1$ | $ - 7$ |
| $0$ | $0$ |
| $1$ | $ - 7$ |
| $2$ | $ - 28$ |

Note: Graph of $y = 7{x^2}$ will open upwards with vertex at centre, focus at $\left( {0,\dfrac{1}{{28}}} \right)$, axis of symmetry $x = 0$ and directrix $y = - \dfrac{1}{{28}}$. It means a mirror image of $y = - 7{x^2}$.
Recently Updated Pages
Can anyone list 10 advantages and disadvantages of friction

What are the Components of Financial System?

How do you arrange NH4 + BF3 H2O C2H2 in increasing class 11 chemistry CBSE

Is H mCT and q mCT the same thing If so which is more class 11 chemistry CBSE

What are the possible quantum number for the last outermost class 11 chemistry CBSE

Is C2 paramagnetic or diamagnetic class 11 chemistry CBSE

Trending doubts
10 examples of friction in our daily life

The correct order of melting point of 14th group elements class 11 chemistry CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

What is the specific heat capacity of ice water and class 11 physics CBSE

State and prove Bernoullis theorem class 11 physics CBSE




