Question

Identify the major arc in the following circle

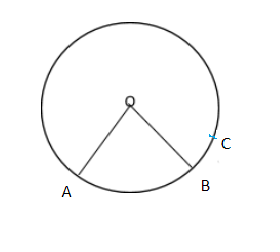
A) Arc \[AOB\]
B) Arc \[BOC\]
C) Arc \[ACB\]
D) Arc \[ABC\]

Answer 1

Hint: Major arc of a circle is an arc which is larger than the semi-circle. Since the semi-circle is nothing but the half of the circle.

Complete step by step answer:

In the given diagram O is the center such that OA and OB are radius which in turn imply that OA=OB. And C is a point in the given circle.
From the given diagram it is clear that the arc AOB and arc BOC are smaller than the semi-circle. Hence they are not considered in this problem.
Now as per the given diagram, we have two arcs here. They are Arc\[ABC\] and Arc \[ACB\]. If we measure the length of the arcs, we can find that the length of arc \[ACB\] is more than the semi-circle and the length of arc \[ABC\] is less than the semi-circle.
Then by the definition of major arc we can conclude that arc \[ACB\] is the major arc whereas the other arcs are non-major arcs

Hence, the correct option is (C) Arc \[ACB\].

Note:
We can measure the length of an arc is the radius and the value of the angle that is made by the end arc and the radius at the centre of the circle is given. The formula will be in the form,
\[s = r\theta \]
Where, \[s\] is the length of the arc, \[r\] be the radius and \[\theta \] be the angle formed by the arc at the circle.
It is clear from the diagram of arcs that Arc\[ACB\] is the major arc.