Question

Identify the name of the triangle.

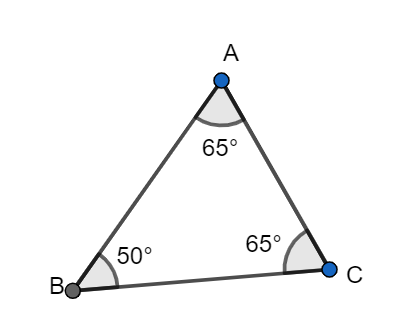
A. acute isosceles triangle
B. acute scalene triangle
C. acute obtuse triangle
D. acute right-angled triangle

Answer 1

Hint: We solve this question by using the basic concepts of triangles in geometry. We need to identify the type of triangle looking at the diagram given. Looking at the angles, we can determine the type of triangle.

Complete step by step solution:
In order to answer this question, let us consider the given triangle. Looking at its angles, we can say that it is definitely an acute triangle since all its angles are less than $90{}^\circ .$ A triangle is said to acute when all its angles are less than $90{}^\circ .$
Next, we see the measure of each angle of the triangle such that $\angle A=65{}^\circ ,\angle B=65{}^\circ ,\angle C=50{}^\circ .$ We can see that the two angles A and B are equal. We also know that the side length of a triangle is proportional to the opposite angle. From the figure, we can see that the angles A and B are equal which means that the sides opposite to these angles are equal. This means that sides BC and AB are equal. A triangle that has two sides of the same length is called an isosceles triangle.
Option A is the correct answer. Option B is not true since for a scalene triangle, all the sides need to be of different length which is not the case in the above figure. Option C is wrong too as an obtuse triangle is one having one of its angles greater than $90{}^\circ .$ Here, none of the angles are above $90{}^\circ .$ Option D is wrong too as it has to have one angle as $90{}^\circ $ for it to be a right-angled triangle.
Hence, the triangle is an acute isosceles triangle and option A is correct.

Note: We need to know the concepts of triangles and the different types of triangles in geometry in order to solve such questions easily. We need to always make sure that the sum of the angles in the triangle adds up to $180{}^\circ .$ If not, then the triangle may have wrong angles.