Question

If a circle cuts a rectangular hyperbola xy = 16 in four points such that the points of intersection lie in the first quadrant. Find the minimum value of the x coordinate of the centre of the circle.

Answer 1

Hint: To solve this question, we will assume that the circle which is cutting the given rectangular hyperbola has the equation: \[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\] where (– g, – f) are the coordinates of the centre. In this equation of the circle, we will put \[y=\dfrac{16}{x}\] to find the intersection points. After this, we will get a biquadratic equation in x. From there, we will find the value of g by equating the coefficient of \[{{x}^{3}}\] to the sum of the roots of the equation. ‘– g’ will be the x coordinate of the centre. Then we will use \[AM\ge GM\] to get its minimum value.

Complete step by step solution:
For a better understanding of the question, let us first see the rough sketch of the hyperbola and the circle.

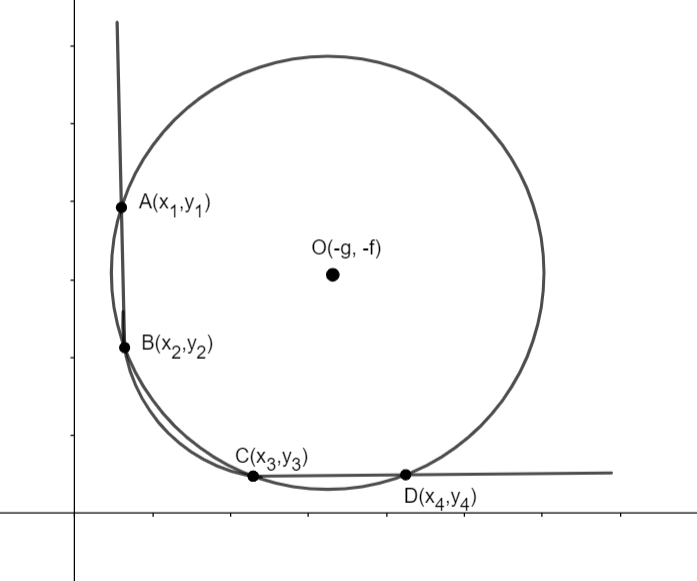
Here, we have drawn a circle which intersects the given rectangular hyperbola at four points. The points of intersection are: \[A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right),C\left( {{x}_{3}},{{y}_{3}} \right),D\left( {{x}_{4}},{{y}_{4}} \right).\] The equation of the circle is \[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\] where O (– g, – f) are the coordinates of the centre. The equation of the hyperbola given is:
\[xy=16.....\left( i \right)\]
\[\Rightarrow y=\dfrac{16}{x}.....\left( ii \right)\]
If we put this value of ‘y’ in the equation of the circle, we will get the intersection points A, B, C and D. Thus, now we will put the value of y from equation (ii) to the equation of the circle. Thus, we will get,
\[{{x}^{2}}+{{\left( \dfrac{16}{x} \right)}^{2}}+2gx+2f\left( \dfrac{16}{x} \right)+c=0\]
\[\Rightarrow {{x}^{2}}+\dfrac{256}{{{x}^{2}}}+2gx+\dfrac{32f}{x}+c=0\]
\[\Rightarrow {{x}^{4}}+256+2g{{x}^{3}}+32fx+c{{x}^{2}}=0\]
\[\Rightarrow {{x}^{4}}+2g{{x}^{3}}+32fx+c{{x}^{2}}+256=0\]
The above obtained equation is a biquadratic equation which has roots \[{{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}}\] which are the x – coordinates of the intersection points A, B, C and D respectively. Now, if we are given a biquadratic equation of the form: \[a{{x}^{4}}+b{{x}^{3}}+c{{x}^{2}}+dx+e=0\] having \[\alpha ,\beta ,\gamma ,\delta ,\] are roots then we have the following relations.
\[\alpha +\beta +\gamma +\delta =\dfrac{-b}{a}\]
\[\alpha \beta \gamma \delta =\dfrac{e}{a}\]
In our case, the roots are: \[{{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}}\] and the coefficient of \[{{x}^{3}}\] in 2g. Thus, we will get,
\[{{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}=\dfrac{-2g}{1}\]
\[\Rightarrow {{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}=-2g.....\left( iii \right)\]
Similarly, the constant term is 256, so we have,
\[{{x}_{1}}{{x}_{2}}{{x}_{3}}{{x}_{4}}=\dfrac{256}{1}\]
\[\Rightarrow {{x}_{1}}{{x}_{2}}{{x}_{3}}{{x}_{4}}=256.....\left( iv \right)\]
Now, we will use the concept of \[AM\ge GM.\] If there are four numbers given, say p, q, r, s, then we can write,
\[\dfrac{p+q+r+s}{4}\ge {{\left( p.q.r.s \right)}^{\dfrac{1}{4}}}\]
Now, we will use the roots of the equation in place of p, q, r and s. Thus, we will get,
\[\dfrac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}}{4}\ge {{\left( {{x}_{1}}{{x}_{2}}{{x}_{3}}{{x}_{4}} \right)}^{\dfrac{1}{4}}}\]
Now, we will put the value of \[{{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}=-2g\] from (iii) to the above inequation. Thus, we will get,
\[\dfrac{-2g}{4}\ge {{\left( {{x}_{1}}{{x}_{2}}{{x}_{3}}{{x}_{4}} \right)}^{\dfrac{1}{4}}}\]
\[\Rightarrow -g\ge 2{{\left( {{x}_{1}}{{x}_{2}}{{x}_{3}}{{x}_{4}} \right)}^{\dfrac{1}{4}}}\]
\[\Rightarrow \text{x-coordinate }\ge 2{{\left( {{x}_{1}}{{x}_{2}}{{x}_{3}}{{x}_{4}} \right)}^{\dfrac{1}{4}}}\]
Now, we will put the value of \[{{x}_{1}}{{x}_{2}}{{x}_{3}}{{x}_{4}}\] from (iv) to the above equation. Thus, we will get,
\[\Rightarrow \text{x-coordinate }\ge 2{{\left( 256 \right)}^{\dfrac{1}{4}}}\]
\[\Rightarrow \text{x-coordinate }\ge 2{{\left( 4\times 4\times 4\times 4 \right)}^{\dfrac{1}{4}}}\]
\[\Rightarrow \text{x-coordinate }\ge 2\times 4\]
\[\Rightarrow \text{x-coordinate }\ge 8\]
Thus, the minimum value of x – coordinate of the centre will be 8.

Note: We have used \[AM\ge GM\] to calculate the minimum value of ‘– g’. We have used the property because all the numbers are positive because the intersection points lie in the first quadrant (so values of all x – coordinates are positive). If the values had been negative, we could not have been able to use this inequality property.